第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
9. 若实数$a$,$b$在数轴上对应的点的位置如图所示,则下列结论中正确的是(
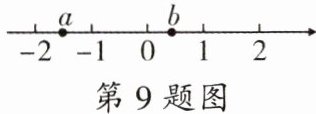
A.$a - b > 0$
B.$-a < b$
C.$a + 1 > b$
D.$a + 1 - b < 0$
D
)
A.$a - b > 0$
B.$-a < b$
C.$a + 1 > b$
D.$a + 1 - b < 0$
答案:
D
10. 小麦同学做这样一道题“计算:$|(-3) + □|$”,其中“$□$”是被墨水污染看不清的一个数,他翻开后面的答案,得知该题计算结果是8,则“$□$”表示的数是(
A.$5$
B.$-5$
C.$11$
D.$-5或11$
D
)A.$5$
B.$-5$
C.$11$
D.$-5或11$
答案:
D
11. 已知两个数的差是25,减数比7的相反数小5,则被减数是
13
.
答案:
13
12. 已知$|a| = 5$,$|b| = 2$,且$a + b < 2$,则$a - b$的值是
-7或-3
.
答案:
-7或-3
13. 高斯被认为是历史上最杰出的数学家之一,享有“数学王子”之称. 现有一种高斯定义的计算式,已知$[x]表示不超过x$的最大整数,如$[3.1] = 3$,$[-0.8] = -1$. 现定义$\{x\} = x + [x]$,如$\{1.5\} = 1.5 + [1.5] = 1.5 + 1 = 2.5$,则$\{2\} - \{-3.7\} = $
11.7
.
答案:
11.7
14. 新情境 北京等5个城市的国际标准时间(单位:h)可在数轴上表示如下:

如果将两地国际标准时间的差简称为时差,回答下列问题:
(1) 伦敦与纽约的时差是几个小时?
(2) 在计算不同城市之间的时差时,有四名学生是这么计算的:
学生1:首尔与纽约的时差为13h;
学生2:首尔与多伦多的时差为13h;
学生3:北京与纽约的时差为14h;
学生4:北京与多伦多的时差为14h;
请你判断一下哪位同学计算的结果是正确的,并说明理由.

如果将两地国际标准时间的差简称为时差,回答下列问题:
(1) 伦敦与纽约的时差是几个小时?
(2) 在计算不同城市之间的时差时,有四名学生是这么计算的:
学生1:首尔与纽约的时差为13h;
学生2:首尔与多伦多的时差为13h;
学生3:北京与纽约的时差为14h;
学生4:北京与多伦多的时差为14h;
请你判断一下哪位同学计算的结果是正确的,并说明理由.
答案:
解:
(1)由数轴可知:伦敦与纽约的时差为0-(-5)=5(h).
(2)由数轴可知:首尔与纽约的时差为9-(-5)=14(h),故学生1计算错误,不符合题意;首尔与多伦多的时差为9-(-4)=13(h),故学生2计算正确,符合题意;北京与纽约的时差为8-(-5)=13(h),故学生3计算错误,不符合题意;北京与多伦多的时差为8-(-4)=12(h),故学生4计算错误,不符合题意,所以学生2计算的结果正确.
(1)由数轴可知:伦敦与纽约的时差为0-(-5)=5(h).
(2)由数轴可知:首尔与纽约的时差为9-(-5)=14(h),故学生1计算错误,不符合题意;首尔与多伦多的时差为9-(-4)=13(h),故学生2计算正确,符合题意;北京与纽约的时差为8-(-5)=13(h),故学生3计算错误,不符合题意;北京与多伦多的时差为8-(-4)=12(h),故学生4计算错误,不符合题意,所以学生2计算的结果正确.
15. 核心素养·运算能力 (1) 已知$|a| = 8$,$|b| = 4$,$a > b$,求$a - b$的值.
(2) 已知$|a| = 9$,$|b| = 6$,$|a - b| = b - a$,求$a - b$的值.
(3) 已知$|a - 3| = 4$,$|b + 5| = 3$,$a < 0$,$b < 0$,求$a - b$的值.
(2) 已知$|a| = 9$,$|b| = 6$,$|a - b| = b - a$,求$a - b$的值.
(3) 已知$|a - 3| = 4$,$|b + 5| = 3$,$a < 0$,$b < 0$,求$a - b$的值.
答案:
解:
(1)因为|a|=8,|b|=4,a>b,所以a=8,b=4或-4,所以a-b=4或12.
(2)因为|a|=9,|b|=6,|a-b|=b-a>0,所以a=-9,b=6或-6,所以a-b=-3或-15.
(3)因为|a-3|=4,a<0,所以a=-1.因为|b+5|=3,b<0,所以b=-2或-8.当a=-1,b=-2时,a-b=-1-(-2)=1;当a=-1,b=-8时,a-b=-1-(-8)=7.综上所述,a-b的值为1或7.
(1)因为|a|=8,|b|=4,a>b,所以a=8,b=4或-4,所以a-b=4或12.
(2)因为|a|=9,|b|=6,|a-b|=b-a>0,所以a=-9,b=6或-6,所以a-b=-3或-15.
(3)因为|a-3|=4,a<0,所以a=-1.因为|b+5|=3,b<0,所以b=-2或-8.当a=-1,b=-2时,a-b=-1-(-2)=1;当a=-1,b=-8时,a-b=-1-(-8)=7.综上所述,a-b的值为1或7.
查看更多完整答案,请扫码查看


