第79页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 填表。
|圆|半径|直径|周长|面积|
|A|5 dm| | | |
|B| |3.2 cm| | |
|C| | |7.536 cm| |

|圆|半径|直径|周长|面积|
|A|5 dm| | | |
|B| |3.2 cm| | |
|C| | |7.536 cm| |

答案:
解析:本题考查圆的半径、直径、周长和面积的计算。需要根据圆的性质以及相关公式来分别计算表格中所缺的数据。圆的直径$d = 2r$($r$为半径),周长$C=\pi d = 2\pi r$,面积$S=\pi r^{2}$。
对于圆A:
已知半径$r = 5dm$,根据直径公式$d = 2r$,可得直径$d=2×5 = 10dm$。
根据周长公式$C=\pi d$,$\pi$取$3.14$,则周长$C = 3.14×10 = 31.4dm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×5^{2}=3.14×25 = 78.5dm^{2}$。
对于圆B:
已知直径$d = 3.2cm$,根据半径公式$r=\frac{d}{2}$,可得半径$r=\frac{3.2}{2}=1.6cm$。
根据周长公式$C=\pi d$,$\pi$取$3.14$,则周长$C = 3.14×3.2 = 10.048cm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×1.6^{2}=3.14×2.56 = 8.0384cm^{2}$。
对于圆C:
已知周长$C = 7.536cm$,根据直径公式$d=\frac{C}{\pi}$,$\pi$取$3.14$,可得直径$d=\frac{7.536}{3.14}=2.4cm$。
根据半径公式$r=\frac{d}{2}$,可得半径$r=\frac{2.4}{2}=1.2cm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×1.2^{2}=3.14×1.44 = 4.5216cm^{2}$。
答案:
|圆|半径|直径|周长|面积|
| ---- | ---- | ---- | ---- | ---- |
|A|5 dm|10 dm|31.4 dm|78.5$dm^{2}$|
|B|1.6 cm|3.2 cm|10.048 cm|8.0384$cm^{2}$|
|C|1.2 cm|2.4 cm|7.536 cm|4.5216$cm^{2}$|
对于圆A:
已知半径$r = 5dm$,根据直径公式$d = 2r$,可得直径$d=2×5 = 10dm$。
根据周长公式$C=\pi d$,$\pi$取$3.14$,则周长$C = 3.14×10 = 31.4dm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×5^{2}=3.14×25 = 78.5dm^{2}$。
对于圆B:
已知直径$d = 3.2cm$,根据半径公式$r=\frac{d}{2}$,可得半径$r=\frac{3.2}{2}=1.6cm$。
根据周长公式$C=\pi d$,$\pi$取$3.14$,则周长$C = 3.14×3.2 = 10.048cm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×1.6^{2}=3.14×2.56 = 8.0384cm^{2}$。
对于圆C:
已知周长$C = 7.536cm$,根据直径公式$d=\frac{C}{\pi}$,$\pi$取$3.14$,可得直径$d=\frac{7.536}{3.14}=2.4cm$。
根据半径公式$r=\frac{d}{2}$,可得半径$r=\frac{2.4}{2}=1.2cm$。
根据面积公式$S=\pi r^{2}$,可得面积$S = 3.14×1.2^{2}=3.14×1.44 = 4.5216cm^{2}$。
答案:
|圆|半径|直径|周长|面积|
| ---- | ---- | ---- | ---- | ---- |
|A|5 dm|10 dm|31.4 dm|78.5$dm^{2}$|
|B|1.6 cm|3.2 cm|10.048 cm|8.0384$cm^{2}$|
|C|1.2 cm|2.4 cm|7.536 cm|4.5216$cm^{2}$|
2. 选择。
(1)一个圆的半径是2 dm,它的周长和面积相比,(
A. 面积大
B. 周长大
C. 一样大
D. 无法比较
(2)一个直径是3 m的圆和一个边长是3 m的正方形,它们的面积相比,(
A. 圆的面积大
B. 正方形的面积大
C. 一样大
D. 无法比较
(1)一个圆的半径是2 dm,它的周长和面积相比,(
D
)。A. 面积大
B. 周长大
C. 一样大
D. 无法比较
(2)一个直径是3 m的圆和一个边长是3 m的正方形,它们的面积相比,(
B
)。A. 圆的面积大
B. 正方形的面积大
C. 一样大
D. 无法比较
答案:
解析:
(1) 对于一个圆,其周长是圆的边界长度,而面积是圆内部的面积大小。周长和面积是两个完全不同的概念,分别用不同的公式计算:周长 $C = 2\pi r$,面积 $A = \pi r^2$。由于它们表示的是不同的几何量,因此不能直接比较大小。
(2) 对于直径为3 m的圆,其半径为1.5 m,面积 $A_{circle} = \pi × (1.5)^2 = 2.25\pi$ $m^2$。对于边长为3 m的正方形,面积 $A_{square} = 3 × 3 = 9$ $m^2$。通过比较这两个面积,我们可以看出正方形的面积大于圆的面积。
答案:
(1) D
(2) B
(1) 对于一个圆,其周长是圆的边界长度,而面积是圆内部的面积大小。周长和面积是两个完全不同的概念,分别用不同的公式计算:周长 $C = 2\pi r$,面积 $A = \pi r^2$。由于它们表示的是不同的几何量,因此不能直接比较大小。
(2) 对于直径为3 m的圆,其半径为1.5 m,面积 $A_{circle} = \pi × (1.5)^2 = 2.25\pi$ $m^2$。对于边长为3 m的正方形,面积 $A_{square} = 3 × 3 = 9$ $m^2$。通过比较这两个面积,我们可以看出正方形的面积大于圆的面积。
答案:
(1) D
(2) B
3. 一个圆形餐桌面的直径是1.8 m,用铝合金条包边,至少需要多长的铝合金条?这个桌面的面积有多大?
答案:
解析:本题主要考查圆的周长和面积的计算。
圆的周长公式为$C = \pi d$,其中$d$为直径,$\pi$取$3.14$。
已知圆形餐桌面的直径$d = 1.8m$,将其代入公式可得:
$C = 3.14×1.8 = 5.652(m)$。
圆的面积公式为$S = \pi r^2$,其中$r$为半径,$r=\frac{d}{2}$。
已知直径$d = 1.8m$,则半径$r = 1.8÷2 = 0.9(m)$。
将半径代入面积公式可得:
$S = 3.14×0.9^2$
$= 3.14×0.81$
$= 2.5434(m^2)$
答案:至少需要$5.652m$长的铝合金条,这个桌面的面积是$2.5434m^2$。
圆的周长公式为$C = \pi d$,其中$d$为直径,$\pi$取$3.14$。
已知圆形餐桌面的直径$d = 1.8m$,将其代入公式可得:
$C = 3.14×1.8 = 5.652(m)$。
圆的面积公式为$S = \pi r^2$,其中$r$为半径,$r=\frac{d}{2}$。
已知直径$d = 1.8m$,则半径$r = 1.8÷2 = 0.9(m)$。
将半径代入面积公式可得:
$S = 3.14×0.9^2$
$= 3.14×0.81$
$= 2.5434(m^2)$
答案:至少需要$5.652m$长的铝合金条,这个桌面的面积是$2.5434m^2$。
4. 一个直径为12 m的圆形喷水池外面有一条宽为2 m的环形小路,这条小路的面积是多少?
答案:
解析:
本题考查圆环的面积计算。需要用到圆面积的计算公式$S = \pi r^{2}$,其中r为圆的半径。
先求出外圆的半径,再求出内圆的半径,然后用外圆的面积减去内圆的面积,即可得到环形小路的面积。
外圆半径:
已知圆形喷水池的直径为12m,则半径为$12 ÷ 2 = 6(m)$。
环形小路的宽度为2m,所以外圆的半径为$6 + 2 = 8(m)$。
内圆半径:
内圆即为喷水池,半径为6m。
计算环形小路的面积:
根据圆的面积公式$S = \pi r^{2}$,可得:
外圆面积为$\pi × 8^{2} = 64\pi (m^{2})$。
内圆面积为$\pi × 6^{2} = 36\pi (m^{2})$。
环形小路的面积为外圆面积减去内圆面积,即:
$64\pi - 36\pi = 28\pi (m^{2})$。
将$\pi$取3.14,得到:
$28\pi \approx 87.92 (m^{2})$。
答案:
这条小路的面积是$87.92 m^{2}$。
本题考查圆环的面积计算。需要用到圆面积的计算公式$S = \pi r^{2}$,其中r为圆的半径。
先求出外圆的半径,再求出内圆的半径,然后用外圆的面积减去内圆的面积,即可得到环形小路的面积。
外圆半径:
已知圆形喷水池的直径为12m,则半径为$12 ÷ 2 = 6(m)$。
环形小路的宽度为2m,所以外圆的半径为$6 + 2 = 8(m)$。
内圆半径:
内圆即为喷水池,半径为6m。
计算环形小路的面积:
根据圆的面积公式$S = \pi r^{2}$,可得:
外圆面积为$\pi × 8^{2} = 64\pi (m^{2})$。
内圆面积为$\pi × 6^{2} = 36\pi (m^{2})$。
环形小路的面积为外圆面积减去内圆面积,即:
$64\pi - 36\pi = 28\pi (m^{2})$。
将$\pi$取3.14,得到:
$28\pi \approx 87.92 (m^{2})$。
答案:
这条小路的面积是$87.92 m^{2}$。
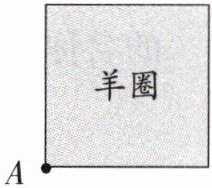
1. 如右图,一块草地中间有一个边长是6 m的正方形羊圈,在墙角A处拴着一只羊,拴羊的绳子长5 m。这只羊最多能吃到多大面积的草?

答案:
解析:本题可根据圆的面积公式,结合羊的活动范围来确定其能吃到草的面积。
由于羊被拴在墙角$A$处,且绳子长$5m$,那么羊的活动范围是$\frac{3}{4}$个以$5m$为半径的圆。
根据圆的面积公式$S = \pi r^2$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$为圆的半径),可求出$\frac{3}{4}$个圆的面积,即羊最多能吃到草的面积。
答案:
$3.14×5^2×\frac{3}{4}$
$=3.14×25×\frac{3}{4}$
$= 78.5×\frac{3}{4}$
$= 58.875$($m^2$)
答:这只羊最多能吃到$58.875m^2$的草。
由于羊被拴在墙角$A$处,且绳子长$5m$,那么羊的活动范围是$\frac{3}{4}$个以$5m$为半径的圆。
根据圆的面积公式$S = \pi r^2$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$为圆的半径),可求出$\frac{3}{4}$个圆的面积,即羊最多能吃到草的面积。
答案:
$3.14×5^2×\frac{3}{4}$
$=3.14×25×\frac{3}{4}$
$= 78.5×\frac{3}{4}$
$= 58.875$($m^2$)
答:这只羊最多能吃到$58.875m^2$的草。
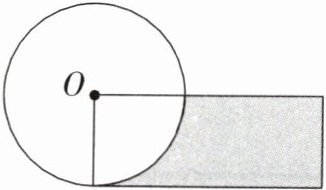
2. 右下图中圆与长方形的面积相等,长方形的长是6.28 m。阴影部分的面积是多少平方米?(提示:设圆的半径是x m,根据圆的面积与长方形的面积相等列方程)

答案:
解析:本题考查了圆与长方形的面积公式,以及如何通过设未知数,根据两者面积相等列方程来求解相关问题,进而得出阴影部分的面积。
设圆的半径是$x$米。
圆的面积公式为$\pi r^2$,这里$r = x$,所以圆的面积为$\pi x^{2}$平方米。
已知长方形的长是$6.28$米,宽就是圆的半径$x$米,长方形面积公式为长乘宽,所以长方形面积为$6.28x$平方米。
因为圆与长方形的面积相等,所以可列方程:
$\pi x^{2}=6.28x$,$\pi$取$3.14$,则$3.14x^{2}=6.28x$,
两边同时除以$x$($x$不为$0$)得到$3.14x = 6.28$,
解得$x = 2$。
阴影部分面积是长方形面积减去圆面积的$\frac{1}{4}$,
圆的面积$S=\pi r^2=3.14×2^2 = 12.56$(平方米),
长方形的面积等于圆的面积也是$12.56$平方米,
那么阴影部分面积$S_{阴}=12.56 - \frac{1}{4}×12.56= 9.42$(平方米)。
答案:$9.42$平方米。
设圆的半径是$x$米。
圆的面积公式为$\pi r^2$,这里$r = x$,所以圆的面积为$\pi x^{2}$平方米。
已知长方形的长是$6.28$米,宽就是圆的半径$x$米,长方形面积公式为长乘宽,所以长方形面积为$6.28x$平方米。
因为圆与长方形的面积相等,所以可列方程:
$\pi x^{2}=6.28x$,$\pi$取$3.14$,则$3.14x^{2}=6.28x$,
两边同时除以$x$($x$不为$0$)得到$3.14x = 6.28$,
解得$x = 2$。
阴影部分面积是长方形面积减去圆面积的$\frac{1}{4}$,
圆的面积$S=\pi r^2=3.14×2^2 = 12.56$(平方米),
长方形的面积等于圆的面积也是$12.56$平方米,
那么阴影部分面积$S_{阴}=12.56 - \frac{1}{4}×12.56= 9.42$(平方米)。
答案:$9.42$平方米。
查看更多完整答案,请扫码查看


