第36页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 根据已知的图示或信息,尝试解答下面两个问题。
(1) 小明$\frac{2}{3}$小时走了2 km。小明每小时走多少千米?
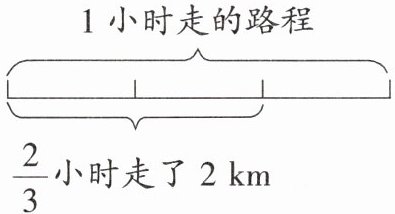
$\frac{2}{3}$小时走了2 km
(2) 小红$\frac{2}{5}$小时走了$\frac{5}{6}$km。小红每小时走多少千米?
(1) 小明$\frac{2}{3}$小时走了2 km。小明每小时走多少千米?

$\frac{2}{3}$小时走了2 km
(2) 小红$\frac{2}{5}$小时走了$\frac{5}{6}$km。小红每小时走多少千米?
答案:
解析:本题可根据速度的计算公式“速度 = 路程÷时间”来分别计算小明和小红的速度,在计算一个数除以分数时,需将其转化为乘以这个分数的倒数来进行计算。
(1)小明的速度为:
$2÷ \frac{2}{3}$
$=2× \frac{3}{2}$
$= 3$(千米/小时)
答案:小明每小时走3千米。
(2)小红的速度为:
$\frac{5}{6}÷ \frac{2}{5}$
$=\frac{5}{6}× \frac{5}{2}$
$=\frac{25}{12}$(千米/小时)
答案:小红每小时走$\frac{25}{12}$千米。
(1)小明的速度为:
$2÷ \frac{2}{3}$
$=2× \frac{3}{2}$
$= 3$(千米/小时)
答案:小明每小时走3千米。
(2)小红的速度为:
$\frac{5}{6}÷ \frac{2}{5}$
$=\frac{5}{6}× \frac{5}{2}$
$=\frac{25}{12}$(千米/小时)
答案:小红每小时走$\frac{25}{12}$千米。
2. 反思:上面两个问题有什么相同的地方与不同的地方? 请尝试总结它们的计算方法。
答案:
解析:
这个问题是反思和总结性质的,不涉及具体的数学计算。它要求对比和分析之前解决的两个问题(可能是关于一个数除以分数的计算问题),找出它们的相同点和不同点,并尝试总结它们的计算方法。
在回答时,可以回顾之前解决的问题,注意以下几点:
相同点:
可能是都涉及到了一个数除以分数的运算。
可能都需要理解分数除法的意义和计算方法。
不同点:
可能是问题的具体情境或数值不同。
可能是解决问题的步骤或策略有所不同。
计算方法总结:
当一个数除以一个分数时,通常可以转化为乘以这个分数的倒数。
需要注意分数的约分和化简。
答案:
相同点:两个问题都涉及到了一个数除以分数的运算,需要理解分数除法的意义和基本方法。
不同点:具体情境、数值或解题步骤可能有所不同。
计算方法:一个数除以一个分数,等于这个数乘以该分数的倒数,并注意分数的约分和化简。
这个问题是反思和总结性质的,不涉及具体的数学计算。它要求对比和分析之前解决的两个问题(可能是关于一个数除以分数的计算问题),找出它们的相同点和不同点,并尝试总结它们的计算方法。
在回答时,可以回顾之前解决的问题,注意以下几点:
相同点:
可能是都涉及到了一个数除以分数的运算。
可能都需要理解分数除法的意义和计算方法。
不同点:
可能是问题的具体情境或数值不同。
可能是解决问题的步骤或策略有所不同。
计算方法总结:
当一个数除以一个分数时,通常可以转化为乘以这个分数的倒数。
需要注意分数的约分和化简。
答案:
相同点:两个问题都涉及到了一个数除以分数的运算,需要理解分数除法的意义和基本方法。
不同点:具体情境、数值或解题步骤可能有所不同。
计算方法:一个数除以一个分数,等于这个数乘以该分数的倒数,并注意分数的约分和化简。
$\frac{3}{8}÷2=\frac{
3
}{8
}○×
\frac{1
}{2
}=($\frac{3}{16}$
)$ $\frac{7}{16}÷\frac{4}{5}=\frac{7
}{16
}○×
\frac{5
}{4
}=($\frac{35}{64}$
)$
答案:
解析:
本题考查一个数除以分数的计算方法。
一个数除以分数,等于这个数乘以分数的倒数。
第一题:
$\frac{3}{8} ÷ 2$
$=\frac{3}{8} × \frac{1}{2}$
$= \frac{3 × 1}{8 × 2}$
$= \frac{3}{16}$
第二题:
$\frac{7}{16} ÷ \frac{4}{5}$
$=\frac{7}{16} × \frac{5}{4}$
$= \frac{7 × 5}{16 × 4}$
$= \frac{35}{64}$
答案:
3. $\frac{3}{8} ÷ 2 = \frac{3}{8} × \frac{1}{2} = \frac{3}{16}$
$\frac{7}{16} ÷ \frac{4}{5} = \frac{7}{16} × \frac{5}{4} = \frac{35}{64}$
本题考查一个数除以分数的计算方法。
一个数除以分数,等于这个数乘以分数的倒数。
第一题:
$\frac{3}{8} ÷ 2$
$=\frac{3}{8} × \frac{1}{2}$
$= \frac{3 × 1}{8 × 2}$
$= \frac{3}{16}$
第二题:
$\frac{7}{16} ÷ \frac{4}{5}$
$=\frac{7}{16} × \frac{5}{4}$
$= \frac{7 × 5}{16 × 4}$
$= \frac{35}{64}$
答案:
3. $\frac{3}{8} ÷ 2 = \frac{3}{8} × \frac{1}{2} = \frac{3}{16}$
$\frac{7}{16} ÷ \frac{4}{5} = \frac{7}{16} × \frac{5}{4} = \frac{35}{64}$
查看更多完整答案,请扫码查看


