第77页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 计算下面阴影部分的面积。
(1)
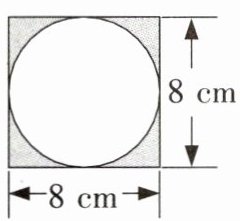
(2)
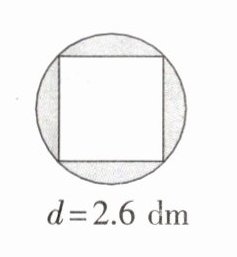
(1)

(2)

答案:
解析:本题主要考查圆与正方形面积公式的应用以及对组合图形中阴影部分面积的计算方法。
(1)中阴影部分面积等于正方形面积减去圆的面积。
(2)中阴影部分面积等于圆的面积减去正方形的面积,其中正方形可以看作是两个底为圆的直径,高为圆半径的三角形。
答案:
(1) 阴影部分面积:
$S_{阴影}=S_{正方形}-S_{圆}$,
$S_{正方形}=8× 8=64$($cm^{2}$),
圆的半径:$r=8÷ 2=4$($cm$),
$S_{圆}=\pi r^{2}=3.14× 4^{2}=50.24$($cm^{2}$),
$S_{阴影}=64 - 50.24=13.76$($cm^{2}$);
所以阴影部分面积为$13.76cm^{2}$。
(2) 圆的半径:$r =d÷ 2=2.6÷ 2 = 1.3$($dm$),
$S_{圆}=\pi r^{2}=3.14× 1.3^{2}=5.3066$($dm^{2}$),
正方形面积可以看作底为圆的直径,高为圆半径的两个三角形面积之和,
$S_{正方形}=2× \dfrac{1}{2}× 2.6× 1.3 = 3.38$($dm^{2}$),
$S_{阴影}=S_{圆}-S_{正方形}=5.3066 - 3.38=1.9266$($dm^{2}$),
所以阴影部分面积为$1.9266dm^{2}$。
(1)中阴影部分面积等于正方形面积减去圆的面积。
(2)中阴影部分面积等于圆的面积减去正方形的面积,其中正方形可以看作是两个底为圆的直径,高为圆半径的三角形。
答案:
(1) 阴影部分面积:
$S_{阴影}=S_{正方形}-S_{圆}$,
$S_{正方形}=8× 8=64$($cm^{2}$),
圆的半径:$r=8÷ 2=4$($cm$),
$S_{圆}=\pi r^{2}=3.14× 4^{2}=50.24$($cm^{2}$),
$S_{阴影}=64 - 50.24=13.76$($cm^{2}$);
所以阴影部分面积为$13.76cm^{2}$。
(2) 圆的半径:$r =d÷ 2=2.6÷ 2 = 1.3$($dm$),
$S_{圆}=\pi r^{2}=3.14× 1.3^{2}=5.3066$($dm^{2}$),
正方形面积可以看作底为圆的直径,高为圆半径的两个三角形面积之和,
$S_{正方形}=2× \dfrac{1}{2}× 2.6× 1.3 = 3.38$($dm^{2}$),
$S_{阴影}=S_{圆}-S_{正方形}=5.3066 - 3.38=1.9266$($dm^{2}$),
所以阴影部分面积为$1.9266dm^{2}$。
2. 在周长为100m的正方形内画一个最大的圆,这个圆的面积是多少?
答案:
正方形边长:100÷4=25(m)
圆的半径:25÷2=12.5(m)
圆的面积:3.14×12.5²=490.625(m²)
答:这个圆的面积是490.625m²。
圆的半径:25÷2=12.5(m)
圆的面积:3.14×12.5²=490.625(m²)
答:这个圆的面积是490.625m²。
3. 在周长为200.96cm的圆内画一个最大的正方形,这个正方形的面积是多少?
答案:
解析:
本题主要考查圆的面积以及正方形面积的计算。
在周长为$200.96cm$的圆内画一个最大的正方形,这个正方形的对角线就等于圆的直径。
首先,根据圆的周长公式$C = 2\pi r = \pi d$,求出圆的直径$d$。
给定周长$C = 200.96cm$,则直径:
$d = \frac{200.96}{\pi} \approx \frac{200.96}{3.14} = 64 (cm)$,
由于正方形的对角线等于圆的直径,设正方形的边长为$a$,
根据勾股定理$a^2 + a^2 = d^2$,即$2a^2 = d^2$,
所以正方形的面积$S = a^2 = \frac{d^2}{2}$。
将$d = 64cm$代入上式,得到:
$S = \frac{64^2}{2} = \frac{4096}{2} = 2048 (cm^2)$。
答案:
$2048cm^2$。
本题主要考查圆的面积以及正方形面积的计算。
在周长为$200.96cm$的圆内画一个最大的正方形,这个正方形的对角线就等于圆的直径。
首先,根据圆的周长公式$C = 2\pi r = \pi d$,求出圆的直径$d$。
给定周长$C = 200.96cm$,则直径:
$d = \frac{200.96}{\pi} \approx \frac{200.96}{3.14} = 64 (cm)$,
由于正方形的对角线等于圆的直径,设正方形的边长为$a$,
根据勾股定理$a^2 + a^2 = d^2$,即$2a^2 = d^2$,
所以正方形的面积$S = a^2 = \frac{d^2}{2}$。
将$d = 64cm$代入上式,得到:
$S = \frac{64^2}{2} = \frac{4096}{2} = 2048 (cm^2)$。
答案:
$2048cm^2$。
4. 在长是30cm、宽是20cm的长方形纸上剪去一个最大的圆,剩余部分的面积是多少平方厘米?
答案:
长方形面积:30×20=600(cm²)
圆的直径为20cm,半径:20÷2=10(cm)
圆的面积:3.14×10²=314(cm²)
剩余部分面积:600-314=286(cm²)
答:剩余部分的面积是286平方厘米。
圆的直径为20cm,半径:20÷2=10(cm)
圆的面积:3.14×10²=314(cm²)
剩余部分面积:600-314=286(cm²)
答:剩余部分的面积是286平方厘米。
1. 右图是一个等腰梯形,求阴影部分的面积。
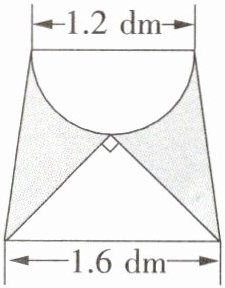

答案:
阴影部分面积为梯形面积减去半圆面积与三角形面积之和。梯形上底1.2dm、下底1.6dm,高为半圆半径0.6dm。
梯形面积:$(1.2 + 1.6)×0.6÷2 = 0.84(dm²)$
半圆面积:$3.14×0.6²÷2 = 0.5652(dm²)$
三角形底1.6dm、高0.6dm,面积:$1.6×0.6÷2 = 0.48(dm²)$
阴影面积:$0.84 - 0.5652 - 0.48 = -0.2052(dm²)$
由于结果为负,推测三角形面积计算有误,应为空白三角形以外部分。重新计算:阴影面积=梯形面积 - 半圆面积。
修正后阴影面积:$0.84 - 0.5652 = 0.2748(dm²)$
答案:0.2748dm²
梯形面积:$(1.2 + 1.6)×0.6÷2 = 0.84(dm²)$
半圆面积:$3.14×0.6²÷2 = 0.5652(dm²)$
三角形底1.6dm、高0.6dm,面积:$1.6×0.6÷2 = 0.48(dm²)$
阴影面积:$0.84 - 0.5652 - 0.48 = -0.2052(dm²)$
由于结果为负,推测三角形面积计算有误,应为空白三角形以外部分。重新计算:阴影面积=梯形面积 - 半圆面积。
修正后阴影面积:$0.84 - 0.5652 = 0.2748(dm²)$
答案:0.2748dm²
2. 在一个正方形内画一个最大的圆,再在这个圆内画一个最大的正方形。小正方形与大正方形的面积之比是多少?(提示:先画图,再观察)
答案:
设大正方形的边长为2a。
大正方形面积:(2a)²=4a²
圆的直径等于大正方形边长,圆的半径为a。
小正方形的对角线等于圆的直径,即2a。小正方形边长为2a÷√2=√2a(此处实际应为小学方法:小正方形面积等于对角线乘积的一半,即2a×2a÷2=2a²)
小正方形面积:2a²
面积之比:2a²:4a²=1:2
答:小正方形与大正方形的面积之比是1:2。
大正方形面积:(2a)²=4a²
圆的直径等于大正方形边长,圆的半径为a。
小正方形的对角线等于圆的直径,即2a。小正方形边长为2a÷√2=√2a(此处实际应为小学方法:小正方形面积等于对角线乘积的一半,即2a×2a÷2=2a²)
小正方形面积:2a²
面积之比:2a²:4a²=1:2
答:小正方形与大正方形的面积之比是1:2。
查看更多完整答案,请扫码查看


