《2025年预学与导学六年级数学上册人教版》

1. 比一比。
(1)爷爷养了鲫鱼和草鱼共1890条,其中草鱼的条数是鲫鱼的2倍。鲫鱼和草鱼各有多少条?
(2)爷爷养了鲫鱼和草鱼共1890条,其中鲫鱼的条数是草鱼的$\frac{1}{2}$。鲫鱼和草鱼各有多少条?

答案：
(1)
解：设鲫鱼有$x$条，则草鱼有$2x$条。
$x + 2x=1890$
$3x=1890$
$x=630$
草鱼：$2x = 2×630 = 1260$（条）
答：鲫鱼有630条，草鱼有1260条。
(2)
解：设草鱼有$x$条，则鲫鱼有$\frac{1}{2}x$条。
$x+\frac{1}{2}x = 1890$
$\frac{3}{2}x=1890$
$x = 1890×\frac{2}{3}$
$x = 1260$
鲫鱼：$\frac{1}{2}x=\frac{1}{2}×1260 = 630$（条）
答：鲫鱼有630条，草鱼有1260条。

2. 一个长方形的周长是64cm,宽是长的$\frac{3}{5}$。这个长方形的面积是多少平方厘米?

答案： 解析：本题可先根据长方形的周长公式以及长和宽的关系求出长方形的长和宽，再根据长方形的面积公式计算出其面积。
步骤一：求长方形长和宽的和
已知长方形的周长是$64cm$，根据长方形周长公式$C=(a + b)×2$（其中$C$表示周长，$a$表示长，$b$表示宽），可得长与宽的和为：$64÷2 = 32cm$。
步骤二：设未知数并求出长方形的长和宽
设长方形的长为$x cm$，因为宽是长的$\frac{3}{5}$，所以宽为$\frac{3}{5}x cm$。
又因为长与宽的和是$32cm$，所以可列方程：$x+\frac{3}{5}x = 32$。
合并同类项：$(1+\frac{3}{5})x = 32$，即$\frac{8}{5}x = 32$。
求解$x$：方程两边同时除以$\frac{8}{5}$，$x = 32÷\frac{8}{5}=32×\frac{5}{8}= 20cm$。
求出宽：宽为$\frac{3}{5}x=\frac{3}{5}×20 = 12cm$。
步骤三：计算长方形的面积
根据长方形面积公式$S = ab$（其中$S$表示面积，$a$表示长，$b$表示宽），可得该长方形的面积为：$20×12 = 240cm^{2}$。
答案：
解：设长方形的长为$x cm$，则宽为$\frac{3}{5}x cm$。
$x+\frac{3}{5}x = 32$
$\frac{8}{5}x = 32$
$x = 32÷\frac{8}{5}=20$
宽：$\frac{3}{5}×20 = 12$（$cm$）
面积：$20×12 = 240$（$cm^{2}$）
答：这个长方形的面积是$240$平方厘米。

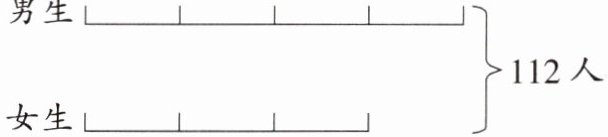
3. 根据下图,用两种不同的方法求出男生人数。

方法1(归一问题)：
方法2(和倍问题)：

答案： 解析：本题考查归一问题和和倍问题的解题方法。
归一问题：先求出单一量（一份量），再求出总量（几份量）。
和倍问题：已知两个数的和以及它们之间的倍数关系，求这两个数。
方法1（归一问题）：
从图中可以看出，男生人数是 4 份，女生人数是 3 份，总人数是$4 + 3 = 7$份，总人数是$112$人。
先求出一份的人数，即$112÷(4 + 3)=112÷7 = 16$人。
男生占$4$份，所以男生人数为$16×4 = 64$人。
方法2（和倍问题）：
设男生人数为$x$人，因为男生人数是$4$份，女生人数是$3$份，所以女生人数是男生人数的$\frac{3}{4}$，即女生人数为$\frac{3}{4}x$人。
根据男女生人数和为$112$人，可列方程：
$x+\frac{3}{4}x = 112$。
合并同类项得$\frac{7}{4}x = 112$。
两边同时除以$\frac{7}{4}$，即$x = 112÷\frac{7}{4}=112×\frac{4}{7}=64$人。
答案：
方法 1：$112÷(4 + 3)=16$（人）
$16×4 = 64$（人）
方法 2：设男生人数为$x$人。
$x+\frac{3}{4}x = 112$
$\frac{7}{4}x = 112$
$x = 112÷\frac{7}{4}=64$（人）
男生人数为$64$人。

甲、乙两地相距480km,客车和货车分别从两地同时出发,相向而行,4小时后相遇,货车的速度是客车的$\frac{3}{5}$。客车和货车的速度分别是多少?

答案： 解析：本题可根据路程、相遇时间和速度和的关系，结合货车速度与客车速度的倍数关系来求解客车和货车的速度。
步骤一：计算客车与货车的速度和
根据公式：速度和$=$路程$÷$相遇时间，已知甲、乙两地相距$480km$，客车和货车$4$小时后相遇，可得客车与货车的速度和为：$480÷4 = 120$（千米/时）
步骤二：设未知数并列出方程
设客车的速度是$x$千米/时，因为货车的速度是客车的$\frac{3}{5}$，所以货车的速度是$\frac{3}{5}x$千米/时。
又因为客车与货车的速度和是$120$千米/时，所以可列方程：$x+\frac{3}{5}x = 120$。
步骤三：解方程求出客车的速度
对$x+\frac{3}{5}x = 120$进行求解：
合并同类项可得：$\frac{8}{5}x = 120$
两边同时除以$\frac{8}{5}$，即$x = 120÷\frac{8}{5}=120×\frac{5}{8} = 75$（千米/时）
步骤四：求出货车的速度
因为货车速度是客车的$\frac{3}{5}$，所以货车速度为：$75×\frac{3}{5} = 45$（千米/时）
答案：
解：设客车的速度是$x$千米/时，则货车的速度是$\frac{3}{5}x$千米/时。
$x+\frac{3}{5}x = 120$
$\frac{8}{5}x = 120$
$x = 120÷\frac{8}{5}=75$
货车速度：$75×\frac{3}{5} = 45$（千米/时）
答：客车的速度是$75$千米/时，货车的速度是$45$千米/时。