《2025年预学与导学六年级数学上册人教版》

1. 填空。
(1)4÷5= (4):(5)= ($\frac{4}{5}$)/( )= (0.8)(填小数)
(2)如果a:b= c,那么a是比的(前项),b是比的(后项),c是比的(比值)。
(3)从A地到B地共180 km,客车要行驶3小时,货车要行驶4小时。
①客车所行驶的路程与时间之比是(180:3),比值是(60)。
②货车所行驶的路程与时间之比是(180:4),比值是(45)。
③客车的速度与货车的速度之比是(4:3),比值是($\frac{4}{3}$)。
④客车行驶的时间与货车行驶的时间之比是(3:4),比值是(0.75)。

答案： 解析：本题主要考查比的意义，包括比与除法、分数的关系，以及比的各部分名称和根据实际情况求比和比值。
(1)根据比与除法的关系$4÷5 = 4:5$；根据分数与除法的关系$4÷5=\frac{4}{5}$；$4÷5 = 0.8$。
(2)在$a:b = c$这个式子中，$a$是比的前项，$b$是比的后项，$c$是比值。
(3)
①客车所行驶的路程与时间之比，根据比的定义，路程与时间的比就是$180:3$，化简比可得$(180÷3):(3÷3)=60:1$，比值是$60÷1 = 60$。
②货车所行驶的路程与时间之比是$180:4$，化简比为$(180÷4):(4÷4)=45:1$，比值是$45÷1 = 45$。
③根据速度 = 路程÷时间，客车速度为$180÷3 = 60$（千米/小时），货车速度为$180÷4 = 45$（千米/小时），所以客车速度与货车速度之比是$60:45$，化简比为$(60÷15):(45÷15)=4:3$，比值是$4÷3=\frac{4}{3}$。
④客车行驶时间与货车行驶时间之比是$3:4$，比值是$3÷4 = 0.75$。
答案：
(1)$4$；$5$；$\frac{4}{5}$；$0.8$；
(2)前项；后项；比值；
(3)①$180:3$；$60$；②$180:4$；$45$；③$4:3$；$\frac{4}{3}$；④$3:4$；$0.75$。

2. 选择。
(1)一杯糖水,糖的质量占糖水质量的1/10。糖与水的质量之比是(A)。
A.1:9 B.1:10 C.9:10 D.9:1
(2)如果长方形的长与宽之比是5:4,那么长比宽多(C)。
A.1/5 B.4/5 C.1/4 D.5/4

答案： 解析：
(1)题目考查比的意义以及比例的计算。
糖的质量占糖水质量的$\frac{1}{10}$，意味着如果糖水总量为10份，糖的质量就是1份，那么水的质量就是$10-1=9(份)$。
因此，糖与水的质量之比是$1:9$。
(2)题目考查比的意义以及比例的计算。
长方形的长与宽之比是$5:4$，我们可以设长为$5x$，宽为$4x$。
长比宽多的长度是$5x - 4x = x$。
所以，长比宽多的比例是$\frac{x}{4x} = \frac{1}{4}$。
答案：
(1)A
(2)C

3. 求比值。
240:12 1.2:0.8 2/3:4/9 0.35:7/8

答案： 解析：本题主要考查求比值的方法，需要用比的前项除以后项来得到比值。
答案：
$240 : 12 = 240 ÷ 12 = 20$
$1.2 : 0.8 = 1.2 ÷ 0.8 = 1.5$
$\frac{2}{3} : \frac{4}{9} = \frac{2}{3} ÷ \frac{4}{9} = \frac{2}{3} × \frac{9}{4} = \frac{3}{2}=1.5$
$0.35 : \frac{7}{8} = 0.35 ÷ \frac{7}{8} = \frac{35}{100} × \frac{8}{7} = \frac{2}{5}=0.4$

1. 如右图,一个面积是$28 cm^2$的平行四边形被分成了3个三角形。这三个三角形的面积之比是多少？

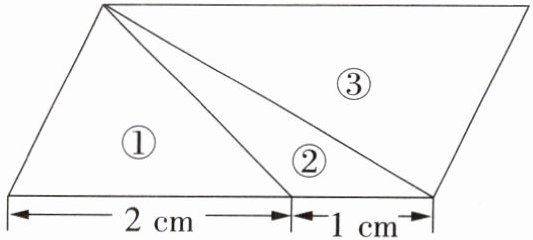
答案： 三个三角形的高相等，均为平行四边形的高h。
三角形①底为2cm，面积：$\frac{1}{2}×2×h = h$
三角形②底为1cm，面积：$\frac{1}{2}×1×h = 0.5h$
三角形③底为$2+1=3$cm，面积：$\frac{1}{2}×3×h = 1.5h$
面积比：$h:0.5h:1.5h = 2:1:3$
答：这三个三角形的面积之比是$2:1:3$。

2. 甲数的3/5与乙数的3/4相等,甲数和乙数的比是(5:4)。

答案： 解析：本题可根据已知条件列出等式，再通过等式的性质求出甲数和乙数的比。
设甲数为$a$，乙数为$b$，已知甲数的$\frac{3}{5}$与乙数的$\frac{3}{4}$相等，则可列出等式$\frac{3}{5}a = \frac{3}{4}b$。
根据比例的基本性质“两内项之积等于两外项之积”，将等式$\frac{3}{5}a = \frac{3}{4}b$转化为$a:b$的形式，即$a:b=\frac{3}{4}:\frac{3}{5}$。
再对$\frac{3}{4}:\frac{3}{5}$进行化简，比的前项和后项同时乘以$20$（$4$和$5$的最小公倍数），得到$(\frac{3}{4}×20):(\frac{3}{5}×20)=15:12 = 5:4$。
答案：$5:4$