第72页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
|轮子名称|半径|直径|周长|
| ---- | ---- | ---- | ---- |
|链轮|
|飞轮|2.5 cm|
|车轮|
与链轮相比,飞轮的半径是链轮的(
| ---- | ---- | ---- | ---- |
|链轮|
7.5 cm
|15 cm|47.1 cm
||飞轮|2.5 cm|
5 cm
|15.7 cm
||车轮|
150 cm
|300 cm
|942 cm|与链轮相比,飞轮的半径是链轮的(
$\frac{1}{3}$
),飞轮的直径是链轮的($\frac{1}{3}$
),飞轮的周长是链轮的($\frac{1}{3}$
);与飞轮相比,车轮的半径是飞轮的(60
)倍,车轮的直径是飞轮的(60
)倍,车轮的周长是飞轮的(60
)倍。
答案:
解析:本题考查圆的半径、直径和周长的关系以及计算。根据$d = 2r$,$C=2\pi r=\pi d$来分别计算链轮、飞轮和车轮的半径、直径和周长,再计算倍数关系。
链轮:
已知链轮直径$d = 15\text{cm}$,根据$d = 2r$,可得半径$r=\frac{d}{2}=\frac{15}{2}=7.5$($\text{cm}$)。
根据$C=\pi d$,取$\pi\approx3.14$,则周长$C = 3.14×15 = 47.1$($\text{cm}$)。
飞轮:
已知飞轮半径$r = 2.5\text{cm}$,根据$d = 2r$,可得直径$d = 2×2.5 = 5$($\text{cm}$)。
根据$C = 2\pi r$,取$\pi\approx3.14$,则周长$C = 2×3.14×2.5 = 15.7$($\text{cm}$)。
车轮:
已知车轮周长$C = 942\text{cm}$,根据$C=\pi d$,可得直径$d=\frac{C}{\pi}=\frac{942}{3.14}=300$($\text{cm}$)。
再根据$d = 2r$,可得半径$r=\frac{d}{2}=\frac{300}{2}=150$($\text{cm}$)。
与链轮相比:
飞轮半径是链轮的:$2.5÷7.5=\frac{1}{3}$。
飞轮直径是链轮的:$5÷15=\frac{1}{3}$。
飞轮周长是链轮的:$15.7÷47.1=\frac{1}{3}$。
与飞轮相比:
车轮半径是飞轮的:$150÷2.5 = 60$。
车轮直径是飞轮的:$300÷5 = 60$。
车轮周长是飞轮的:$942÷15.7 = 60$。
答案:
|轮子名称|半径|直径|周长|
| ---- | ---- | ---- | ---- |
|链轮|7.5 cm|15 cm|47.1 cm|
|飞轮|2.5 cm|5 cm|15.7 cm|
|车轮|150 cm|300 cm|942 cm|
$\frac{1}{3}$;$\frac{1}{3}$;$\frac{1}{3}$;60;60;60。
链轮:
已知链轮直径$d = 15\text{cm}$,根据$d = 2r$,可得半径$r=\frac{d}{2}=\frac{15}{2}=7.5$($\text{cm}$)。
根据$C=\pi d$,取$\pi\approx3.14$,则周长$C = 3.14×15 = 47.1$($\text{cm}$)。
飞轮:
已知飞轮半径$r = 2.5\text{cm}$,根据$d = 2r$,可得直径$d = 2×2.5 = 5$($\text{cm}$)。
根据$C = 2\pi r$,取$\pi\approx3.14$,则周长$C = 2×3.14×2.5 = 15.7$($\text{cm}$)。
车轮:
已知车轮周长$C = 942\text{cm}$,根据$C=\pi d$,可得直径$d=\frac{C}{\pi}=\frac{942}{3.14}=300$($\text{cm}$)。
再根据$d = 2r$,可得半径$r=\frac{d}{2}=\frac{300}{2}=150$($\text{cm}$)。
与链轮相比:
飞轮半径是链轮的:$2.5÷7.5=\frac{1}{3}$。
飞轮直径是链轮的:$5÷15=\frac{1}{3}$。
飞轮周长是链轮的:$15.7÷47.1=\frac{1}{3}$。
与飞轮相比:
车轮半径是飞轮的:$150÷2.5 = 60$。
车轮直径是飞轮的:$300÷5 = 60$。
车轮周长是飞轮的:$942÷15.7 = 60$。
答案:
|轮子名称|半径|直径|周长|
| ---- | ---- | ---- | ---- |
|链轮|7.5 cm|15 cm|47.1 cm|
|飞轮|2.5 cm|5 cm|15.7 cm|
|车轮|150 cm|300 cm|942 cm|
$\frac{1}{3}$;$\frac{1}{3}$;$\frac{1}{3}$;60;60;60。
2. 从上题的例子中,你发现两个不同的圆相比较,它们的周长、直径、半径之间有怎样的关系呢?
答案:
解析:
本题主要考查圆的周长公式以及圆的基本性质。
首先,需要知道圆的周长是如何计算的。一个圆的周长是 $C = 2\pi r$,其中 $r$ 是圆的半径。而圆的直径 $d$ 是半径的两倍,即 $d = 2r$;
接下来,考虑两个不同的圆。假设第一个圆的半径为 $r_1$,周长为 $C_1$;第二个圆的半径为 $r_2$,周长为 $C_2$。根据圆的周长公式,有:
$C_1 = 2\pi r_1$,
$C_2 = 2\pi r_2$,
如果两个圆的半径之比是 $\frac{r_1}{r_2}$,那么它们的周长之比也是相同的,即:
$\frac{C_1}{C_2} = \frac{2\pi r_1}{2\pi r_2} = \frac{r_1}{r_2}$,
同样地,由于直径是半径的两倍,所以两个圆的直径之比也是 $\frac{d_1}{d_2} = \frac{2r_1}{2r_2} = \frac{r_1}{r_2}$。
答案:
两个不同的圆相比较,如果它们的半径之比为 $\frac{r_1}{r_2}$,则它们的周长之比和直径之比也都是 $\frac{r_1}{r_2}$。即两个圆的周长、直径、半径之间的比例是相等的。
本题主要考查圆的周长公式以及圆的基本性质。
首先,需要知道圆的周长是如何计算的。一个圆的周长是 $C = 2\pi r$,其中 $r$ 是圆的半径。而圆的直径 $d$ 是半径的两倍,即 $d = 2r$;
接下来,考虑两个不同的圆。假设第一个圆的半径为 $r_1$,周长为 $C_1$;第二个圆的半径为 $r_2$,周长为 $C_2$。根据圆的周长公式,有:
$C_1 = 2\pi r_1$,
$C_2 = 2\pi r_2$,
如果两个圆的半径之比是 $\frac{r_1}{r_2}$,那么它们的周长之比也是相同的,即:
$\frac{C_1}{C_2} = \frac{2\pi r_1}{2\pi r_2} = \frac{r_1}{r_2}$,
同样地,由于直径是半径的两倍,所以两个圆的直径之比也是 $\frac{d_1}{d_2} = \frac{2r_1}{2r_2} = \frac{r_1}{r_2}$。
答案:
两个不同的圆相比较,如果它们的半径之比为 $\frac{r_1}{r_2}$,则它们的周长之比和直径之比也都是 $\frac{r_1}{r_2}$。即两个圆的周长、直径、半径之间的比例是相等的。
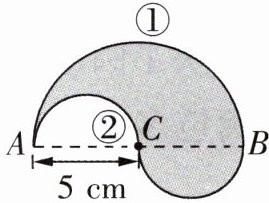
3. 如右图,C为AB的中点,从点A到点B有两条路可以走,请分别计算这两条路的长度。
根据上面的计算结果,我猜想:
|我有新发现:|我要求助:|
| | |
建议:课内预学,时间5分钟。

根据上面的计算结果,我猜想:
|我有新发现:|我要求助:|
| | |
建议:课内预学,时间5分钟。
答案:
设小圆半径为$r$,大圆半径为$R$。由图可知$AC = 5\space cm$,$C$为$AB$中点,所以$AB=2AC = 10\space cm$,即$R=5\space cm$,$r=\frac{AC}{2}=2.5\space cm$。
路①长度:为大半圆周长,$l_1=\frac{1}{2}×2\pi R=\pi R = 3.14×5 = 15.7\space cm$。
路②长度:为两个小半圆周长之和,$l_2=2×\frac{1}{2}×2\pi r=2\pi r=2×3.14×2.5 = 15.7\space cm$。
两条路长度均为$15.7\space cm$。
我猜想:从点$A$到点$B$的两条路长度相等。
路①长度:为大半圆周长,$l_1=\frac{1}{2}×2\pi R=\pi R = 3.14×5 = 15.7\space cm$。
路②长度:为两个小半圆周长之和,$l_2=2×\frac{1}{2}×2\pi r=2\pi r=2×3.14×2.5 = 15.7\space cm$。
两条路长度均为$15.7\space cm$。
我猜想:从点$A$到点$B$的两条路长度相等。
查看更多完整答案,请扫码查看


