第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
2. $1+3+5+7+9+11+9+7+5+3+1=$(
61
)
答案:
$1+3+5+7+9+11+9+7+5+3+1$
$=(1+3+5+7+9+11)+(9+7+5+3+1)$
$=6^2 + 5^2$
$=36 + 25$
$=61$
61
$=(1+3+5+7+9+11)+(9+7+5+3+1)$
$=6^2 + 5^2$
$=36 + 25$
$=61$
61
1. A、B、C、D、E五人进行围棋比赛,每两人之间都要下一盘。A已经下了4盘,B下了3盘,C下了2盘,D下了1盘,那么E一共下了几盘?分别是和谁下的?
答案:
解析:
这是一个组合与逻辑推理问题,考察的是如何在给定条件下确定每个人下棋的盘数和对手。
首先,理解题目条件:五人每两人之间都要下一盘棋,A下了4盘,B下了3盘,C下了2盘,D下了1盘。
接下来,我们按照逻辑进行推理:
1. A下了4盘,意味着A与B、C、D、E各下了一盘,因为总共有四个人可以和A下棋。
2. D下了1盘,由于A已经和所有人都下过棋,所以D这1盘棋一定是和A下的。
3. B下了3盘,由于D只和A下了棋,所以B没有和D下棋。B的3盘棋一定是和A、C、E下的。
4. C下了2盘,根据前面的推理,C已经和A、B各下了一盘棋,因此C没有和D、E下棋。
5. 现在我们来确定E下了几盘棋。根据前面的推理,E已经和A下了一盘棋(因为A和所有人都下过棋),E还和B下了一盘棋(因为B下了3盘棋,其中一盘是和A下的,另外两盘只能和C、E下,而C只下了2盘棋,所以其中一盘是和B下的)。
综上所述,E一共下了2盘棋,分别是和A、B下的。
答案:
E一共下了2盘棋,分别是和A、B下的。
这是一个组合与逻辑推理问题,考察的是如何在给定条件下确定每个人下棋的盘数和对手。
首先,理解题目条件:五人每两人之间都要下一盘棋,A下了4盘,B下了3盘,C下了2盘,D下了1盘。
接下来,我们按照逻辑进行推理:
1. A下了4盘,意味着A与B、C、D、E各下了一盘,因为总共有四个人可以和A下棋。
2. D下了1盘,由于A已经和所有人都下过棋,所以D这1盘棋一定是和A下的。
3. B下了3盘,由于D只和A下了棋,所以B没有和D下棋。B的3盘棋一定是和A、C、E下的。
4. C下了2盘,根据前面的推理,C已经和A、B各下了一盘棋,因此C没有和D、E下棋。
5. 现在我们来确定E下了几盘棋。根据前面的推理,E已经和A下了一盘棋(因为A和所有人都下过棋),E还和B下了一盘棋(因为B下了3盘棋,其中一盘是和A下的,另外两盘只能和C、E下,而C只下了2盘棋,所以其中一盘是和B下的)。
综上所述,E一共下了2盘棋,分别是和A、B下的。
答案:
E一共下了2盘棋,分别是和A、B下的。
2. 观察下图中●的个数。
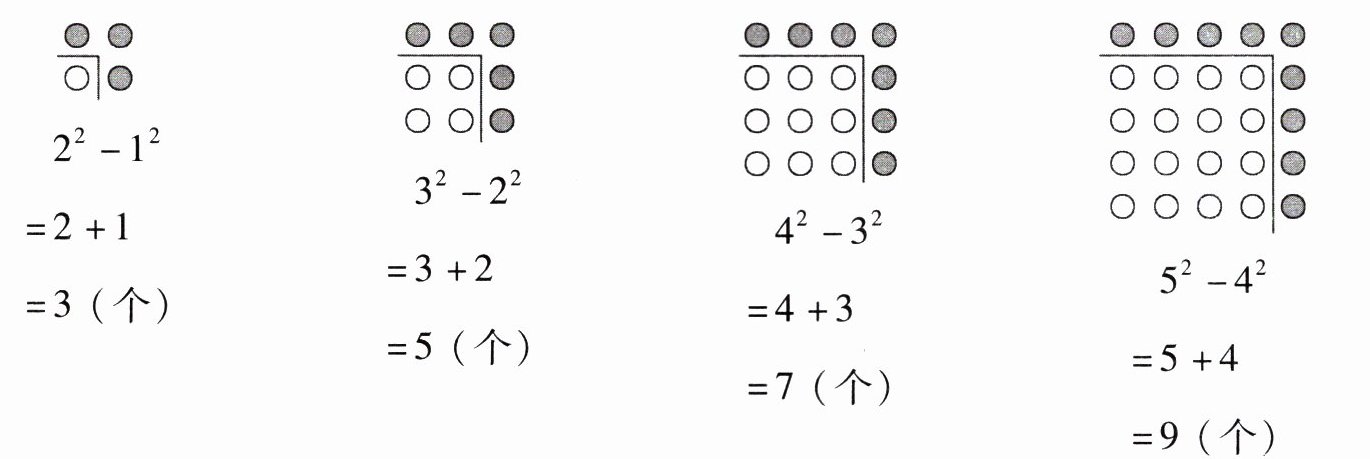
照这样的规律画下去,第6个图形有几个●?
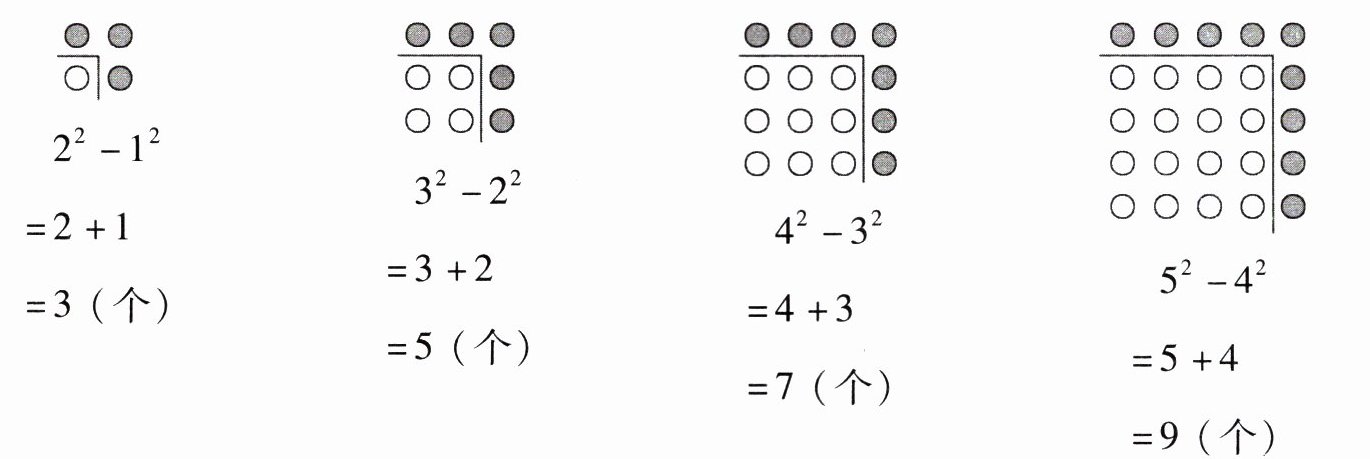
照这样的规律画下去,第6个图形有几个●?
答案:
解析:
本题考查根据图形规律和算式规律找出第$6$个图形中$●$的个数。
观察所给算式和图形:
$2^{2}-1^{2}=2 + 1=3$(个),对应图形中$●$有$3$个;
$3^{2}-2^{2}=3 + 2=5$(个),对应图形中$●$有$5$个;
$4^{2}-3^{2}=4 + 3=7$(个),对应图形中$●$有$7$个;
$5^{2}-4^{2}=5 + 4=9$(个),对应图形中$●$有$9$个。
可以发现规律为:第$n$个图形中$●$的个数等于$(n + 1)^{2}-n^{2}$,且$(n + 1)^{2}-n^{2}=(n + 1)+n$。
当$n = 6$时,$(6 + 1)^{2}-6^{2}=7 + 6=13$(个)。
答案:
第$6$个图形有$13$个$●$。
本题考查根据图形规律和算式规律找出第$6$个图形中$●$的个数。
观察所给算式和图形:
$2^{2}-1^{2}=2 + 1=3$(个),对应图形中$●$有$3$个;
$3^{2}-2^{2}=3 + 2=5$(个),对应图形中$●$有$5$个;
$4^{2}-3^{2}=4 + 3=7$(个),对应图形中$●$有$7$个;
$5^{2}-4^{2}=5 + 4=9$(个),对应图形中$●$有$9$个。
可以发现规律为:第$n$个图形中$●$的个数等于$(n + 1)^{2}-n^{2}$,且$(n + 1)^{2}-n^{2}=(n + 1)+n$。
当$n = 6$时,$(6 + 1)^{2}-6^{2}=7 + 6=13$(个)。
答案:
第$6$个图形有$13$个$●$。
根据上面的规律,计算下面的式子。
$10^{2}-9^{2}+9^{2}-8^{2}+8^{2}-7^{2}+… +2^{2}-1^{2}$
$10^{2}-9^{2}+9^{2}-8^{2}+8^{2}-7^{2}+… +2^{2}-1^{2}$
答案:
$10^{2}-9^{2}+9^{2}-8^{2}+8^{2}-7^{2}+\ldots +2^{2}-1^{2}$
$=10^{2}+(-9^{2}+9^{2})+(-8^{2}+8^{2})+\ldots +(-2^{2}+2^{2})-1^{2}$
$=10^{2}-1^{2}$
$=100 - 1$
$=99$
答案:99
$=10^{2}+(-9^{2}+9^{2})+(-8^{2}+8^{2})+\ldots +(-2^{2}+2^{2})-1^{2}$
$=10^{2}-1^{2}$
$=100 - 1$
$=99$
答案:99
查看更多完整答案,请扫码查看


