《2025年云南省标准教辅同步指导训练与检测六年级数学上册人教版》

1. 如图,将一个圆分成若干(偶数)等份,剪开后,拼成一个近似于长方形的图形。从图中可以看出,如果圆的半径是r,那么长方形的长是(πr),宽是(r)。因为$S_{长方形}= $(πr)×(r),所以$S_{圆}= $(πr)×(r)= (πr²)。

答案： 本题可根据圆拼成近似长方形的过程，结合长方形面积公式来推导圆的面积公式。
将一个圆分成若干（偶数）等份，剪开后拼成一个近似于长方形的图形。
这个长方形的长近似于圆周长的一半，圆的周长公式为$C = 2\pi r$，那么圆周长的一半就是$\pi r$，所以长方形的长是$\pi r$。
这个长方形的宽近似于圆的半径$r$。
因为长方形的面积公式为$S = 长×宽$，已知长方形的长是$\pi r$，宽是$r$，所以$S_{长方形}=\pi r× r$。
由于这个长方形是由圆拼成的，它们的面积相等，所以$S_{圆}=\pi r× r=\pi r^{2}$。
故答案依次为：$\pi r$；$r$；$\pi r$；$r$；$\pi r$；$r$；$\pi r^{2}$。

2. 一个圆的直径是10cm,它的周长是(31.4)cm,面积是(78.5)$cm^{2}$。

答案： 解析：
本题考查圆的周长和面积的计算。
圆的周长公式为：$C = \pi d$，其中d是圆的直径。
圆的面积公式为：$S = \pi r^{2}$，其中r是圆的半径。
根据题目，圆的直径为10cm，所以半径$r = \frac{d}{2} = \frac{10}{2} = 5(cm)$。
代入公式进行计算：
圆的周长：$C = \pi × 10 = 10\pi \approx 31.4(cm)$；
圆的面积：$S = \pi × 5^{2} = 25\pi \approx 78.5({cm}^{2})$。
答案：
31.4；78.5。

3. 公园草坪上一个自动旋转喷灌装置的射程是8m,它能喷灌的面积是(200.96)$m^{2}$。

答案： 解析：本题考查圆的面积公式的应用。自动旋转喷灌装置的射程就是圆的半径，根据圆的面积公式$S = \pi r^{2}$（其中$S$表示圆的面积，$\pi$通常取$3.14$，$r$为圆的半径），已知半径$r = 8m$，则喷灌面积$S=3.14×8^{2}=3.14×64 = 200.96$（$m^{2}$）。
答案：$200.96$。

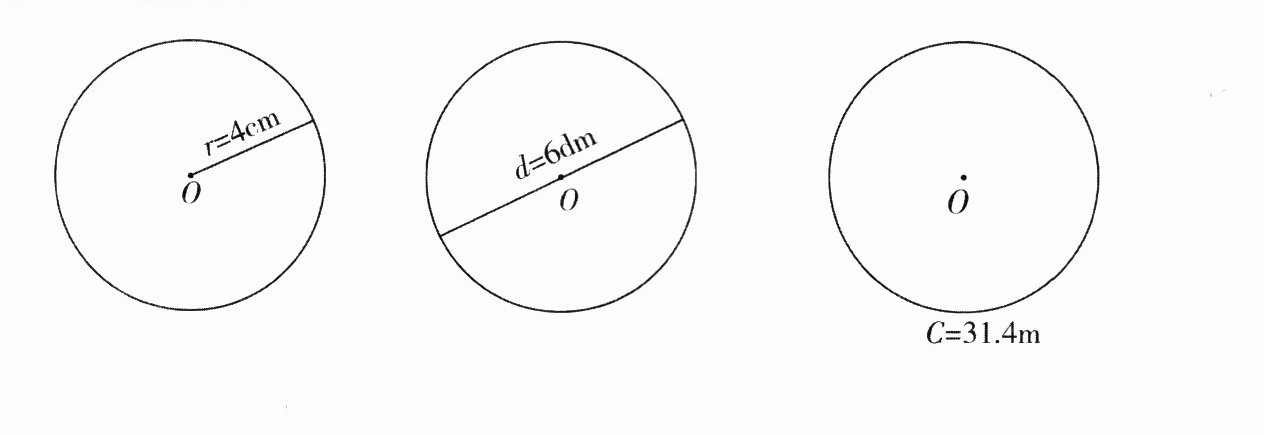
二、计算下面各圆的面积。

答案： 第一个圆（$r = 4cm$）
圆的面积公式为$S=\pi r^{2}$，$\pi$取$3.14$。
解：将$r = 4cm$代入公式$S=\pi r^{2}$，可得$S = 3.14×4^{2}=3.14×16 = 50.24cm^{2}$。
第二个圆（$d = 6dm$）
先求半径$r=\frac{d}{2}=\frac{6}{2}=3dm$，再根据圆的面积公式$S=\pi r^{2}$，$\pi$取$3.14$。
解：将$r = 3dm$代入公式$S=\pi r^{2}$，可得$S=3.14×3^{2}=3.14×9 = 28.26dm^{2}$。
第三个圆（$C = 31.4m$）
先根据圆的周长公式$C = 2\pi r$求半径$r$，$\pi$取$3.14$，则$r=\frac{C}{2\pi}=\frac{31.4}{2×3.14}=5m$，再根据圆的面积公式$S=\pi r^{2}$。
解：将$r = 5m$代入公式$S=\pi r^{2}$，可得$S = 3.14×5^{2}=3.14×25=78.5m^{2}$。
综上，三个圆的面积分别为$\boldsymbol{50.24cm^{2}}$、$\boldsymbol{28.26dm^{2}}$、$\boldsymbol{78.5m^{2}}$。

1. 大、小两个圆的半径之比是2:1,它们的面积之比是(C)。
A.1:2
B.1:4
C.4:1

答案： 解析：本题可根据圆的面积公式分别表示出大圆和小圆的面积，再求它们的面积之比。
步骤一：明确圆的面积公式
圆的面积公式为$S = \pi r^2$（其中$S$表示圆的面积，$r$表示圆的半径）。
步骤二：设出大圆和小圆的半径
已知大、小两个圆的半径之比是$2:1$，可设小圆半径为$r$，那么大圆半径就是$2r$。
步骤三：分别计算大圆和小圆的面积
大圆面积$S_1$：根据圆的面积公式，将大圆半径$2r$代入可得$S_1 = \pi(2r)^2 = 4\pi r^2$。
小圆面积$S_2$：将小圆半径$r$代入圆的面积公式可得$S_2 = \pi r^2$。
步骤四：计算大圆和小圆的面积之比
求$S_1$与$S_2$的比，即$\frac{S_1}{S_2}=\frac{4\pi r^2}{\pi r^2}=4:1$。
答案：C

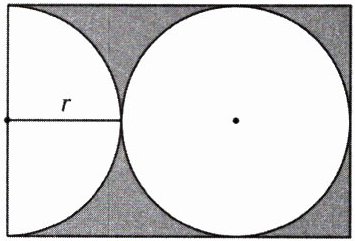
2. 右图中长方形的面积是(B)。

A.6r
B.$6r^{2}$
C.$\frac{3}{2}\pi r^{2}$

答案： 本题考查长方形面积的计算。
从图中可以看出这是一个长方形，长方形的长是$3r$，宽是$2r$。
长方形的面积公式为：$面积 = 长 × 宽$。
代入数据可得：
$长方形的面积= 3r × 2r = 6r^{2}$。
故答案为B。