《2025年云南省标准教辅同步指导训练与检测六年级数学上册人教版》

1. 在一块边长为8dm的正方形纸板中剪下一个半径最大的圆。纸板剩下的面积是多大？

答案： 正方形面积：8×8=64(dm²)
圆的半径：8÷2=4(dm)
圆的面积：3.14×4²=50.24(dm²)
剩下面积：64-50.24=13.76(dm²)
答：纸板剩下的面积是13.76dm²。

2. 一个工业零件的横截面如图中的阴影部分,请计算这个零件的横截面的面积。

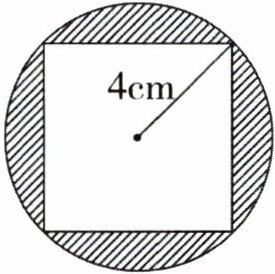
答案： 3.14×4² - 4×4×2 = 18.24(cm²)

3. 如图,李叔叔家有一块长方形菜地,他在菜地里挖了一个半圆形的鱼塘,其余的地方种了草莓。种草莓的面积有多大？

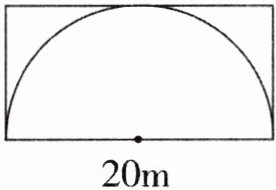
答案： 解析：本题考查圆的面积公式和长方形面积公式的应用。
先分别算出长方形和半圆的面积，再用长方形的面积减去半圆的面积，即可得到种草莓的面积。
长方形的长为$20$米，宽为半圆的半径$20÷2 = 10$米。
根据长方形面积公式$S = a× b$（其中$S$为长方形面积，$a$为长，$b$为宽），可得长方形面积为$20×(20÷2)= 20×10 = 200$（平方米）。
已知半圆直径为$20$米，则半径$r = 20÷2 = 10$米。
根据圆的面积公式$S=\pi r^{2}$（其中$S$为圆的面积，$\pi$通常取$3.14$，$r$为半径），可得半圆面积为$\frac{1}{2}×3.14×(20÷2)^{2}=\frac{1}{2}×3.14×10^{2}=\frac{1}{2}×3.14×100 = 157$（平方米）。
种草莓的面积等于长方形面积减去半圆面积，即$20×(20÷2)-\frac{1}{2}×3.14×(20÷2)^{2}= 200 - 157 = 43$（平方米）。
答案：$20×(20÷2)-\frac{1}{2}×3.14×(20÷2)^{2}= 200 - 157 = 43$（平方米），
答：种草莓的面积是$43$平方米。

1. 用一根铁丝恰好给半径是10dm的圆形桌子围了一圈。用这根铁丝围成一个最大的正方形,这个正方形的面积是多少平方分米？

答案： 解析：本题可先根据圆的半径求出圆的周长，此周长即为铁丝的长度，也就是正方形的周长，再根据正方形周长公式求出边长，最后根据正方形面积公式求出面积。
答案：
圆的周长：$C = 2×3.14×10 = 62.8$（分米）
正方形边长：$62.8÷4 = 15.7$（分米）
正方形面积：$15.7×15.7 = 246.49$（平方分米）
答：这个正方形的面积是$246.49$平方分米。

2. 如图,圆的周长是24cm,圆的面积等于长方形的面积。图中涂色部分的周长是多少厘米？(提示：涂色部分的周长= 长方形的长×2+圆的周长×1/4。)

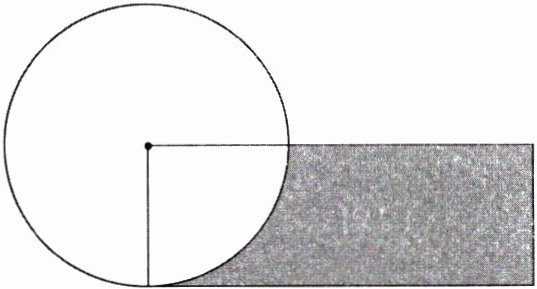
答案： 解析：本题考查圆的周长和面积公式的综合应用，以及图形周长的计算。
设圆的半径为$r$。
已知圆的周长是$24cm$，根据圆的周长公式$C = 2\pi r$，可得$2\pi r=24$。
因为圆的面积等于长方形的面积，圆的面积公式为$S=\pi r^{2}$，设长方形的长为$a$，宽为$r$，则长方形面积$S = ar=\pi r^{2}$，所以$a = \pi r$。
求涂色部分的周长，根据提示“涂色部分的周长 = 长方形的长×2 + 圆的周长×$\frac{1}{4}$”。
长方形的长为$\pi r$，圆的周长为$24cm$，则涂色部分周长$C_{阴影}=2\pi r+\frac{1}{4}×24$。
把$2\pi r = 24$代入上式，可得$C_{阴影}=24 + 6=30$（$cm$）。
答案：$30cm$。