《2025年云南省标准教辅同步指导训练与检测六年级数学上册人教版》

一、找出下面每句话中的单位“1”,并写出数量关系式。
1. 甲数是乙数的$\frac{2}{3}$。
这里把(乙数)看作单位“1”,(乙数)×$\frac{2}{3}$= (甲数)。
2. 修路队已经修了一条路总长的$\frac{5}{7}$。
这里把(一条路的总长)看作单位“1”,(一条路的总长)×$\frac{5}{7}$= (已修的路长)。
3. 成人体内水分的质量约占体重的$\frac{2}{3}$。
这里把(体重)看作单位“1”,(体重)×$\frac{2}{3}$= (体内水分的质量)。
4. 冰融化成水后,水的体积是冰的体积的$\frac{9}{10}$。
这里把(冰的体积)看作单位“1”,(冰的体积)×$\frac{9}{10}$= (水的体积)。

答案： 解析：
1. 题目考查的是对单位“1”的理解以及数量关系的建立。在每句话中，我们需要找到一个基准量，这个基准量就是单位“1”。然后，根据题目给出的比例关系，我们可以建立起数量关系式。
答案：
1. 这里把(乙数)看作单位“1”，(乙数)×$\frac{2}{3}$ = (甲数)。
2. 这里把(一条路的总长)看作单位“1”，(一条路的总长)×$\frac{5}{7}$ = (已修的路长)。
3. 这里把(体重)看作单位“1”，(体重)×$\frac{2}{3}$ = (体内水分的质量)。
4. 这里把(冰的体积)看作单位“1”，(冰的体积)×$\frac{9}{10}$ = (水的体积)。

二、看图列式计算。
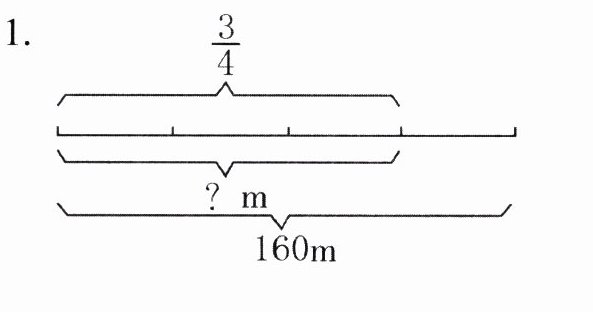
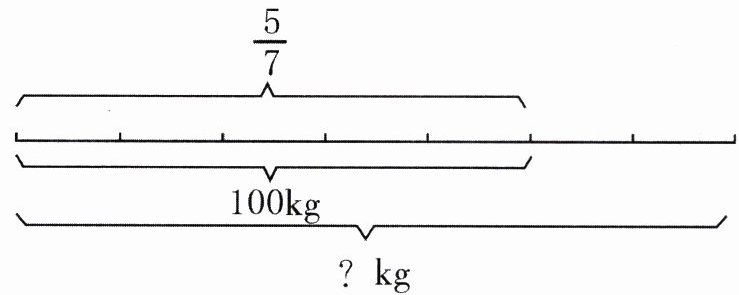
1. $160×(1 - \frac{3}{4})= 160×\frac{1}{4}= 40$（$m$）
2.
$100÷\frac{5}{7}= 100×\frac{7}{5}= 140$（$kg$）

答案： 二、1.
解析：考查利用分数除法解决实际问题。从图中可知总长度为$160m$，将其看作单位“1”，求的部分占总长度的$1 - \frac{3}{4}$，用总长度乘以该分率即可求出结果。
答案：$160×(1 - \frac{3}{4})$
$= 160×\frac{1}{4}$
$= 40$（$m$）
2.
解析：考查利用分数除法解决实际问题。从图中可知$100kg$占总重量的$\frac{5}{7}$，把总重量看作单位“1”，根据已知一个数的几分之几是多少，求这个数用除法，用$100$除以$\frac{5}{7}$可求出总重量。
答案：$100÷\frac{5}{7}$
$= 100×\frac{7}{5}$
$= 140$（$kg$）

三、解方程。
$\frac{6}{7}x= \frac{4}{5}$ $x-\frac{2}{5}x= 9$ $x+\frac{2}{7}x= 540$

答案： $\frac{6}{7}x=\frac{4}{5}$
解：$x=\frac{4}{5}÷\frac{6}{7}$
$x=\frac{4}{5}×\frac{7}{6}$
$x=\frac{14}{15}$
$x-\frac{2}{5}x=9$
解：$\frac{3}{5}x=9$
$x=9÷\frac{3}{5}$
$x=9×\frac{5}{3}$
$x=15$
$x+\frac{2}{7}x=540$
解：$\frac{9}{7}x=540$
$x=540÷\frac{9}{7}$
$x=540×\frac{7}{9}$
$x=420$