第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
一、直接写出得数。
$\frac{15}{7}×\frac{21}{20}=$
$\frac{4}{7}×\frac{21}{10}=$
$16×\frac{7}{8}=$
$\frac{2}{3}×\frac{5}{7}=$
$\frac{3}{4}×\frac{5}{8}×\frac{16}{15}=$
$\frac{7}{9}×\frac{18}{11}×\frac{22}{21}=$
$\frac{7}{6}×\frac{9}{10}×\frac{2}{3}=$
$\frac{15}{7}×\frac{21}{20}=$
$\frac{9}{4}$
$\frac{4}{7}×\frac{21}{10}=$
$\frac{6}{5}$
$16×\frac{7}{8}=$
14
$\frac{2}{3}×\frac{5}{7}=$
$\frac{10}{21}$
$\frac{3}{4}×\frac{5}{8}×\frac{16}{15}=$
$\frac{1}{2}$
$\frac{7}{9}×\frac{18}{11}×\frac{22}{21}=$
$\frac{4}{3}$
$\frac{7}{6}×\frac{9}{10}×\frac{2}{3}=$
$\frac{7}{10}$
答案:
解析:
题目考查的是分数的乘法运算,涉及到分数的相乘以及约分等知识点。
对于分数的乘法,直接将分子相乘作为新的分子,分母相乘作为新的分母,再进行约分。
答案:
$\frac{15}{7} × \frac{21}{20} = \frac{9}{4}$
$\frac{4}{7} × \frac{21}{10} = \frac{6}{5}$
$16 × \frac{7}{8} = 14$
$\frac{2}{3} × \frac{5}{7} = \frac{10}{21}$
$\frac{3}{4} × \frac{5}{8} × \frac{16}{15} = \frac{1}{2}$
$\frac{7}{9} × \frac{18}{11} × \frac{22}{21} = \frac{4}{3}$
$\frac{7}{6} × \frac{9}{10} × \frac{2}{3} = \frac{7}{10}$
题目考查的是分数的乘法运算,涉及到分数的相乘以及约分等知识点。
对于分数的乘法,直接将分子相乘作为新的分子,分母相乘作为新的分母,再进行约分。
答案:
$\frac{15}{7} × \frac{21}{20} = \frac{9}{4}$
$\frac{4}{7} × \frac{21}{10} = \frac{6}{5}$
$16 × \frac{7}{8} = 14$
$\frac{2}{3} × \frac{5}{7} = \frac{10}{21}$
$\frac{3}{4} × \frac{5}{8} × \frac{16}{15} = \frac{1}{2}$
$\frac{7}{9} × \frac{18}{11} × \frac{22}{21} = \frac{4}{3}$
$\frac{7}{6} × \frac{9}{10} × \frac{2}{3} = \frac{7}{10}$
二、找出下面每句话中的单位“1”。
1. 男生人数是女生的$\frac{5}{6}$。(
2. 鸡的数量比鸭多$\frac{1}{4}$。(
3. 实际用量比计划用量节约了$\frac{2}{7}$。(
4. 一种电视机降价了$\frac{1}{6}$。(
1. 男生人数是女生的$\frac{5}{6}$。(
女生人数
)是单位“1”。2. 鸡的数量比鸭多$\frac{1}{4}$。(
鸭的数量
)是单位“1”。3. 实际用量比计划用量节约了$\frac{2}{7}$。(
计划用量
)是单位“1”。4. 一种电视机降价了$\frac{1}{6}$。(
这种电视机原来的价格
)是单位“1”。
答案:
解析:本题考查的是如何找单位“1”,可根据判断单位“1”的方法来逐一分析各句。
判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”。
1. 男生人数是女生的$\frac{5}{6}$,这里是把女生人数和男生人数作比较,说男生人数是女生人数的$\frac{5}{6}$,“是”后面是女生人数,所以女生人数是单位“1”。
2. 鸡的数量比鸭多$\frac{1}{4}$,此句是鸡的数量和鸭的数量作比较,说鸡的数量比鸭多$\frac{1}{4}$,“比”后面是鸭的数量,所以鸭的数量是单位“1”。
3. 实际用量比计划用量节约了$\frac{2}{7}$,这是实际用量和计划用量作比较,说实际用量比计划用量节约$\frac{2}{7}$,“比”后面是计划用量,所以计划用量是单位“1”。
4. 一种电视机降价了$\frac{1}{6}$,这里是将电视机现在的价格和原来的价格作比较,说电视机降价了$\frac{1}{6}$,“降价”是相对于原来的价格而言的,也就是“的”字前面是原来的价格,所以这种电视机原来的价格是单位“1”。
答案:
1. 女生人数;
2. 鸭的数量;
3. 计划用量;
4. 这种电视机原来的价格。
判断单位“1”的方法:一般是把“比、占、是、相当于”后面的量看作单位“1”,即分数“的”字前面的量看作单位“1”。
1. 男生人数是女生的$\frac{5}{6}$,这里是把女生人数和男生人数作比较,说男生人数是女生人数的$\frac{5}{6}$,“是”后面是女生人数,所以女生人数是单位“1”。
2. 鸡的数量比鸭多$\frac{1}{4}$,此句是鸡的数量和鸭的数量作比较,说鸡的数量比鸭多$\frac{1}{4}$,“比”后面是鸭的数量,所以鸭的数量是单位“1”。
3. 实际用量比计划用量节约了$\frac{2}{7}$,这是实际用量和计划用量作比较,说实际用量比计划用量节约$\frac{2}{7}$,“比”后面是计划用量,所以计划用量是单位“1”。
4. 一种电视机降价了$\frac{1}{6}$,这里是将电视机现在的价格和原来的价格作比较,说电视机降价了$\frac{1}{6}$,“降价”是相对于原来的价格而言的,也就是“的”字前面是原来的价格,所以这种电视机原来的价格是单位“1”。
答案:
1. 女生人数;
2. 鸭的数量;
3. 计划用量;
4. 这种电视机原来的价格。
三、看图列式计算。
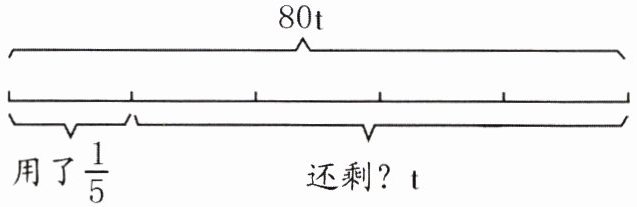
1.
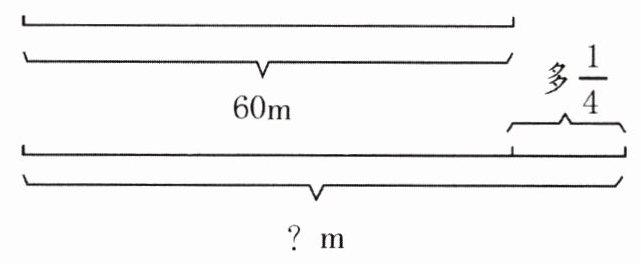
2.
1.

$80×(1-\frac{1}{5})=64$
2.

$60×(1+\frac{1}{4})=75$
答案:
1. $80×(1-\frac{1}{5})=64$
2. $60×(1+\frac{1}{4})=75$
2. $60×(1+\frac{1}{4})=75$
四、根据算式补充条件。
果园里有桃树120棵, 。梨树有多少棵?
1. $120×\frac{1}{5}$,条件:(
2. $120×(1+\frac{1}{5})$,条件:(
3. $120×(1-\frac{1}{5})$,条件:(
果园里有桃树120棵, 。梨树有多少棵?
1. $120×\frac{1}{5}$,条件:(
梨树棵数是桃树棵数的$\frac{1}{5}$
)。2. $120×(1+\frac{1}{5})$,条件:(
梨树比桃树多$\frac{1}{5}$
)。3. $120×(1-\frac{1}{5})$,条件:(
梨树比桃树少$\frac{1}{5}$
)。
答案:
解析:本题考查根据算式补充条件,关键在于分析算式中数量关系,确定所求梨树棵数与桃树棵数的联系。
1. 对于算式$120×\frac{1}{5}$,是用桃树的棵数乘以$\frac{1}{5}$,所以补充的条件是梨树棵数是桃树棵数的$\frac{1}{5}$。
2. 对于算式$120×(1+\frac{1}{5})$,$1+\frac{1}{5}$表示比$1$多$\frac{1}{5}$,也就是梨树棵数比桃树棵数多$\frac{1}{5}$,所以补充的条件是梨树比桃树多$\frac{1}{5}$。
3. 对于算式$120×(1-\frac{1}{5})$,$1-\frac{1}{5}$表示比$1$少$\frac{1}{5}$,即梨树棵数比桃树棵数少$\frac{1}{5}$,所以补充的条件是梨树比桃树少$\frac{1}{5}$。
答案:
1. 梨树棵数是桃树棵数的$\frac{1}{5}$;
2. 梨树比桃树多$\frac{1}{5}$;
3. 梨树比桃树少$\frac{1}{5}$。
1. 对于算式$120×\frac{1}{5}$,是用桃树的棵数乘以$\frac{1}{5}$,所以补充的条件是梨树棵数是桃树棵数的$\frac{1}{5}$。
2. 对于算式$120×(1+\frac{1}{5})$,$1+\frac{1}{5}$表示比$1$多$\frac{1}{5}$,也就是梨树棵数比桃树棵数多$\frac{1}{5}$,所以补充的条件是梨树比桃树多$\frac{1}{5}$。
3. 对于算式$120×(1-\frac{1}{5})$,$1-\frac{1}{5}$表示比$1$少$\frac{1}{5}$,即梨树棵数比桃树棵数少$\frac{1}{5}$,所以补充的条件是梨树比桃树少$\frac{1}{5}$。
答案:
1. 梨树棵数是桃树棵数的$\frac{1}{5}$;
2. 梨树比桃树多$\frac{1}{5}$;
3. 梨树比桃树少$\frac{1}{5}$。
查看更多完整答案,请扫码查看


