《2025年名师帮同步学案九年级数学全一册人教版》

11.(例2)“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,人径2尺,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题.它的示意图如图所示,则井深$BD=$7.5尺.

答案： 7.5

12.李华晚上在两根相距40 m的路灯杆下来回散步,如图,已知李华身高$AB=1.6m$,灯柱$CD=EF=8m.$
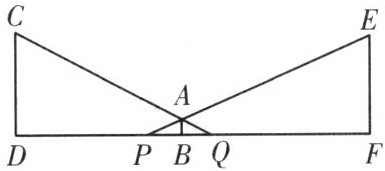
(1)若李华距灯柱CD的距离$DB=16m$,求他的影子BQ的长;
(2)若李华的影子$PB=5m$,求李华距灯柱CD的距离.

答案： 解:
(1)
∵AB//CD,
∴△ABQ∽△CDQ,
∴$\frac{AB}{CD}$=$\frac{BQ}{DQ}$,即$\frac{1.6}{8}$=$\frac{BQ}{16+BQ}$,
∴BQ=4m;
(2)
∵AB//EF,
∴△ABP∽△EFP,
∴$\frac{AB}{EF}$=$\frac{PB}{PF}$,即$\frac{1.6}{8}$=$\frac{5}{PF}$,
∴PF=25m,
∵DF=40m,
∴BD=20m.
　答:李华距灯柱CD的距离是20m.

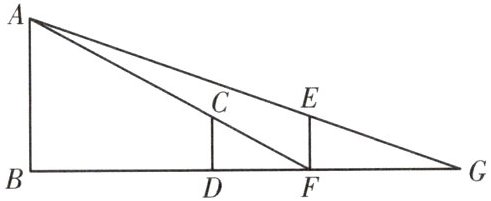
13.如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小华在点D处测得自己的影长$DF=3m$,沿BD方向到达点F处再测得自己的影长$FG=4m$.如果小华的身高为1.5 m,求路灯杆AB的高度.

答案： 解:
∵CD//EF//AB,
　可以得到△CDF∽△ABF,
　△ABG∽△EFG,
∴$\frac{CD}{AB}$=$\frac{DF}{BF}$,$\frac{EF}{AB}$=$\frac{FG}{BG}$,
　又
∵CD=EF,
∴$\frac{DF}{BF}$=$\frac{FG}{BG}$,
∵DF=3m,FG=4m,BF=BD+DF=BD+3,BG=BD+DF+FG=BD+7,
∴$\frac{3}{BD+3}$=$\frac{4}{BD+7}$,
∴BD=9,BF=9+3=12m,
∴$\frac{1.5}{AB}$=$\frac{3}{12}$,
　解得AB=6m.
　答:路灯杆AB的高度是6m.