第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.如图,已知二次函数的图象过三个点$A(-1,0)$,$B(3,0)$,$C(0,-3)$.
(1)求这个二次函数的解析式;
(2)求抛物线的对称轴;
(3)求抛物线的顶点坐标.
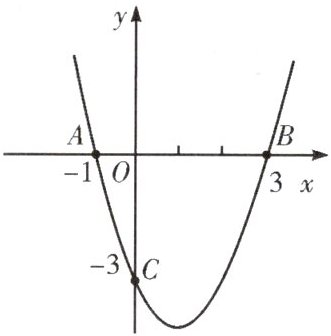
(1)求这个二次函数的解析式;
(2)求抛物线的对称轴;
(3)求抛物线的顶点坐标.

答案:
解:
(1)
∵二次函数图象过点A(−1,0)和B (3,0),
∴设二次函数的解析式为y=a(x+1)(x−3),把C(0,−3)代入,得a(0+1)(0−3)=−3,a=1,
∴y=(x+1)(x−3)=x²−2x−3;
(2)
∵y=x²−2x−3=x²−2x+1−4=(x−1)²−4,
∴抛物线的对称轴x=1;
(3)
∵y=(x−1)²−4,
∴抛物线的顶点坐标为(1,−4).
(1)
∵二次函数图象过点A(−1,0)和B (3,0),
∴设二次函数的解析式为y=a(x+1)(x−3),把C(0,−3)代入,得a(0+1)(0−3)=−3,a=1,
∴y=(x+1)(x−3)=x²−2x−3;
(2)
∵y=x²−2x−3=x²−2x+1−4=(x−1)²−4,
∴抛物线的对称轴x=1;
(3)
∵y=(x−1)²−4,
∴抛物线的顶点坐标为(1,−4).
2.如图,已知抛物线$y=x^{2}-2x-3$与$x$轴交于点$A$,$B$,与$y$轴交于点$C$.
(1)求点$A$,$B$,$C$的坐标;
(2)求$S_{\triangle ABC}$;
(3)若点$P$在抛物线上,且$S_{\triangle ABP}=S_{\triangle ABC}$,求点$P$的坐标.
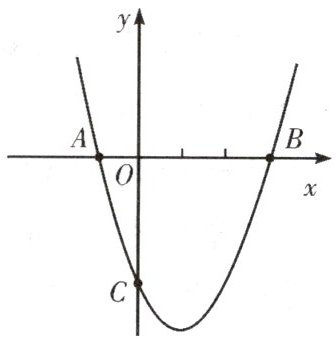
(1)求点$A$,$B$,$C$的坐标;
(2)求$S_{\triangle ABC}$;
(3)若点$P$在抛物线上,且$S_{\triangle ABP}=S_{\triangle ABC}$,求点$P$的坐标.

答案:
解:
(1)当x=0时,y=−3,
∴C(0,−3),
当y=0时,x²−2x−3=0,
(x−3)(x+1)=0,
x₁=3或x₂=−1,
∴A(−1,0),B(3,0);
(2)
∵A(−1,0),B(3,0),
∴AB=3 + 1 = 4,
∵C(0,−3),
∴OC=3,
∴S△ABC=$\frac{1}{2}$AB·OC=$\frac{1}{2}$×4×3 = 6;
(3)当y=3时,x²−2x−3=3,
x²−2x=6,
(x−1)²=7,
x−1=±$\sqrt{7}$,
x=1±$\sqrt{7}$
当y=−3时,x²−2x−3=−3,
x²−2x=0,
x₁=0(舍去),x₂=2.
∴点P的坐标(1+$\sqrt{7}$,3)或(1−$\sqrt{7}$,3)或(2,−3).
(1)当x=0时,y=−3,
∴C(0,−3),
当y=0时,x²−2x−3=0,
(x−3)(x+1)=0,
x₁=3或x₂=−1,
∴A(−1,0),B(3,0);
(2)
∵A(−1,0),B(3,0),
∴AB=3 + 1 = 4,
∵C(0,−3),
∴OC=3,
∴S△ABC=$\frac{1}{2}$AB·OC=$\frac{1}{2}$×4×3 = 6;
(3)当y=3时,x²−2x−3=3,
x²−2x=6,
(x−1)²=7,
x−1=±$\sqrt{7}$,
x=1±$\sqrt{7}$
当y=−3时,x²−2x−3=−3,
x²−2x=0,
x₁=0(舍去),x₂=2.
∴点P的坐标(1+$\sqrt{7}$,3)或(1−$\sqrt{7}$,3)或(2,−3).
查看更多完整答案,请扫码查看


