第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
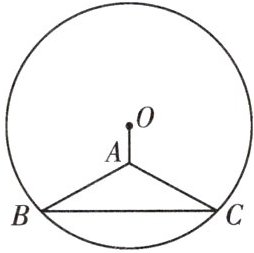
1.(例1)如图,已知等腰△ABC的顶角顶点A在⊙O的内部,点B,C在⊙O上,连OA,求证:OA⊥BC.

答案:
证明:如图,连接OB,OC,OA并延长交BC于点D,

∵OB = OC,OA = OA,AB = AC,
∴△OBA≌△OCA(SSS),
∴∠BOA = ∠COA,
∴OD⊥BC,
∴OA⊥BC.
证明:如图,连接OB,OC,OA并延长交BC于点D,

∵OB = OC,OA = OA,AB = AC,
∴△OBA≌△OCA(SSS),
∴∠BOA = ∠COA,
∴OD⊥BC,
∴OA⊥BC.
2.已知射线OM经过⊙O的圆心,与⊙O相交于点A,点B在⊙O上,且∠BOA=30°,点P为射线OM上异于点O的一动点,直线PB交⊙O于点C,且PC=OC.
(1)如图1,当点P在线段OA上时,求∠PBO的度数;
(2)如图2,当点P在线段OA的延长线上时,则∠PBO的度数为______(直接写出结果).
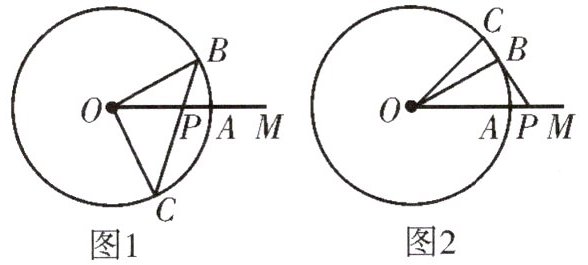
(1)解:∵OB = OC,∴∠C = ∠PBO.
设∠PBO = ∠C = x,∵PC = OC,
∴∠COP = ∠CPO = ∠B + ∠BOA = x + 30°,
在△POC中,x + 2(x + 30°) = 180°,
∴x = 40°,
∴∠PBO = 40°.
(2)
(1)如图1,当点P在线段OA上时,求∠PBO的度数;
(2)如图2,当点P在线段OA的延长线上时,则∠PBO的度数为______(直接写出结果).

(1)解:∵OB = OC,∴∠C = ∠PBO.
设∠PBO = ∠C = x,∵PC = OC,
∴∠COP = ∠CPO = ∠B + ∠BOA = x + 30°,
在△POC中,x + 2(x + 30°) = 180°,
∴x = 40°,
∴∠PBO = 40°.
(2)
100°
答案:
(1)解:
∵OB = OC,
∴∠C = ∠PBO.
设∠PBO = ∠C = x,
∵PC = OC,
∴∠COP = ∠CPO = ∠B + ∠BOA = x + 30°,
在△POC中,x + 2(x + 30°) = 180°,
∴x = 40°,
∴∠PBO = 40°.
(2)100°
(1)解:
∵OB = OC,
∴∠C = ∠PBO.
设∠PBO = ∠C = x,
∵PC = OC,
∴∠COP = ∠CPO = ∠B + ∠BOA = x + 30°,
在△POC中,x + 2(x + 30°) = 180°,
∴x = 40°,
∴∠PBO = 40°.
(2)100°
查看更多完整答案,请扫码查看


