《2025年名师帮同步学案九年级数学全一册人教版》

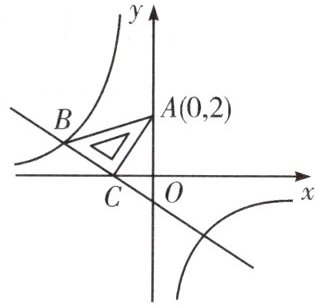
10. 如图, 将一块等腰直角三角板$ABC$放在第二象限, 斜靠在两坐标轴上, 点$C$坐标为$(-1,0)$,$A(0,2)$, 一次函数$y=kx+b$的图象经过点$B,C$, 反比例函数$y=\frac {m}{x}$的图象经过点$B$.
(1) 求一次函数和反比例函数的解析式;
(2) 直接写出当$x＜0$时,$kx+b-\frac {m}{x}＜0$的解集;
(3) 在$x$轴上找一点$M$, 使得$AM+BM$的值最小, 并求出点$M$的坐标.

答案：
解:
(1)如图①，过点$B$作$BF⊥x$轴于点$F$。

$\because$点$C$坐标为$(-1,0)$，点$A$坐标为$(0,2)$，$\therefore OA=2$，$OC=1$。
$\because ∠BCA=90°$，
$\therefore ∠BCF+∠ACO=90°$。
又$\because ∠CAO+∠ACO=90°$，
$\therefore ∠BCF=∠CAO$。
在$\triangle AOC$和$\triangle CFB$中，$\begin{cases}∠CAO=∠BCF\\∠AOC=∠CFB=90°\\AC=BC\end{cases}$
$\therefore\triangle AOC\cong\triangle CFB(AAS)$。
$\therefore FC=OA=2$，$BF=OC=1$。
$\therefore$点$B$的坐标为$(-3,1)$，将点$B$的坐标代入$y=\frac{m}{x}$，可得$m=-3$。
$\therefore$反比例函数解析式为$y=-\frac{3}{x}$。
将点$B$，$C$的坐标代入一次函数解析式中，可得$\begin{cases}-3k+b=1\\-k+b=0\end{cases}$，解得$\begin{cases}k=-\frac{1}{2}\\b=-\frac{1}{2}\end{cases}$。
$\therefore$一次函数解析式为$y=-\frac{1}{2}x-\frac{1}{2}$。
(2)$-3＜x＜0$。
(3)如图②，作点$A$关于$x$轴的对称点$A'$，连接$BA'$与$x$轴的交点为点$M$。

$\because A(0,2)$，
$\therefore A'(0,-2)$。
设直线$A'B$的解析式为$y=ax+b(a≠0)$，将点$A'$及点$B$的坐标代入，可得$\begin{cases}-3a+b=1\\b=-2\end{cases}$，解得$\begin{cases}a=-1\\b=-2\end{cases}$。
$\therefore$直线$A'B$的解析式为$y=-x-2$。
令$y=0$，可得$-x-2=0$，
解得$x=-2$。
故点$M$的坐标为$(-2,0)$。
综上所述，点$M$的坐标为$(-2,0)$时，$AM+BM$的值最小。