《2025年名师帮同步学案九年级数学全一册人教版》

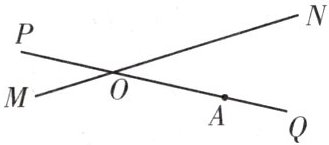
26.如图,铁路MN和公路PQ在点O处交汇,$∠QON=30^{\circ }$,在点A处有一栋居民楼,$AO=240m$,如果火车行驶时周围200m以内会受到噪音的影响,当火车以72 km/h的速度行驶时,居民楼受噪音影响的时间为多少秒?

答案：
解：如图，以点A 为圆心，$200 \mathrm { m } $为半径画圆，与M N 交于点B ，点D ，

过点A 作$A C \perp M N ，$
$\because \angle Q O N = 30 ^ { \circ } ，$$O A = 240 \mathrm { m } ，$$\therefore A C = 120 \mathrm { m } ．$
当火车到B 点时对A 处产生噪音影响，到点D 时结束影响，此时$A B = 200 \mathrm { m } ，$
$\because A B = 200 \mathrm { m } ，$$A C = 120 \mathrm { m } ，$$\therefore $由勾股定理得$B C = 160 \mathrm { m } ．$
$\therefore B D = 2 B C = 320 \mathrm { m } ，$$\because 72 \mathrm { km / h } = 20 \mathrm { m / s } ，$
$\therefore $影响时间$t = \frac { s } { v } = 16 \mathrm { s } ．$

27.如图,AE的延长线和$△ABC$的外接圆$\odot O$相交于点D.
(1)若点E是$△ABC$的内心,求证:$DB=DC=DE;$
(2)若$DB=DC=DE$,求证:点E是$△ABC$的内心.

答案：
证明：（1）连接$$B E $$，$$C E $$，如图．

$\because $$ 点$$E $$ 是$$\triangle A B C $$ 的内心，$
\therefore \angle B A D = \angle C A D $$，$$\angle A B E = \angle C B E $$，
$\angle A C E = \angle B C E $$，又$$\because \$$\angle CBD = \angle CAD$$，$$\angle BCD = \angle BAD$$，$
\therefore \angle BED = \angle BAD + \angle ABE = \angle CAD + \angle CBE$$，
$\angle DBE = \angle CBD + \angle CBE = \angle CAD + \angle CBE$$，$\angle CED = \angle CAD + \angle ACE = \angle BAD + \angle BCE$$，
$\angle DCE = \angle BCD + \angle BCE = \angle BAD + \angle BCE$$，$
\therefore \angle BED = \angle DBE$$，$$\angle CED = \angle DCE$$，
$\therefore \triangle BDE$$ 是等腰三角形，$$\triangle CED$$ 是等腰三角形，$
\therefore DE = DB$$，$$DE = DC$$，
$\therefore DB = DC = DE$$；（2）$$\because BD = CD$$，$
\therefore \overparen{BD} = \overparen{CD}$$．
$\therefore \angle 1 = \angle 2$$，$
\because BD = DE$$，
$\therefore \angle DBE = \angle DEB$$，$
\because \angle DBE = \angle 4 + \angle 5$$，
$\angle DEB = \angle 3 + \angle 2$$，$$\angle 5 = \angle 1$$，$
\therefore \angle 3 = \angle 4$$．
$\therefore AE$$ 平分$$\angle BAC$$，$$BE$$ 平分$$\angle ABC$$，$
\therefore$$ 点$$E$$ 为$$\triangle ABO$$ 的内心。