《2025年名师帮同步学案九年级数学全一册人教版》

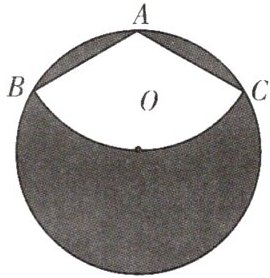
23.(例13)如图,有一个直径为1m的圆形铁皮,圆心为O,要从中间剪去一个$120^{\circ }$的扇形ABC,且$\widehat {BC}$经过点O.
(1)求剪掉后阴影部分的面积;
(2)若用所留的扇形ABC铁皮围成一个圆锥,该圆锥的底面积的半径是多少?

答案：
（例 13）解：（1）如图，连接O A ，O B ．由$\angle B A C = 120 ^ { \circ } ，$可知$A B = \frac { 1 } { 2 } \mathrm { m } ，$点O 在扇形A B C 的$\overparen { B C } $上，

$\therefore $扇形A B C 的面积为$\frac { 120 } { 360 } \pi × \left( \frac { 1 } { 2 } \right) ^ { 2 } = \frac { \pi } { 12 } ( \mathrm { m } ^ { 2 } ) ，$$\therefore $剪掉后阴影部分的面积为
$\pi × \left( \frac { 1 } { 2 } \right) ^ { 2 } - \frac { \pi } { 12 } = \frac { \pi } { 6 } ( \mathrm { m } ^ { 2 } ) ；$（2）由$2 \pi r = \frac { 120 } { 180 } \pi × \frac { 1 } { 2 } ，$得$r = \frac { 1 } { 6 } ，$即圆锥底面圆的半径是$\frac { 1 } { 6 } \mathrm { m } ．$

24.如图①,在正方形铁皮上剪下一个扇形和一个半径为1 cm的圆形,使之恰好围成如图②所示的一个圆锥,求圆锥的高.

答案： 解：$\because $半径为$1 \mathrm { cm } $的圆形，
$\therefore $底面圆的半径为$1 \mathrm { cm } ，$周长为$2 \pi \mathrm { cm } ，$扇形弧长为$2 \pi = \frac { 90 \pi × R } { 180 } ，$$\therefore R = 4 ，$即母线为$4 \mathrm { cm } ，$
$\therefore $圆锥的高为$\sqrt { 16 - 1 } = \sqrt { 15 } \mathrm { cm } ．$

25.(例14)已知点P在抛物线$y=-x^{2}+4$上,$\odot P$的半径为1,当$\odot P$与坐标轴相切时,求点P坐标.

答案： （例 14）解：①当$\odot P $与x 轴相切时，
当y = 1 时，即$1 = - x ^ { 2 } + 4 ，$
$ - x ^ { 2 } + 3 = 0 ，$$x _ { 1 } = \sqrt { 3 } ，$$x _ { 2 } = - \sqrt { 3 } ．$
此时点P 的坐标为$( \sqrt { 3 } , 1 ) ，$$( - \sqrt { 3 } , 1 ) ．$
当y = - 1 时，即$ - 1 = - x ^ { 2 } + 4 ，$$ - x ^ { 2 } + 5 = 0 ，$$x _ { 1 } = \sqrt { 5 } ，$$x _ { 2 } = - \sqrt { 5 } ，$
此时点P 的坐标为$( \sqrt { 5 } , - 1 ) ，$$( - \sqrt { 5 } , - 1 ) ．$
②当$\odot P $与y 轴相切时，有
$x _ { 1 } = 1 ，$$x _ { 2 } = - 1 ，$当$x _ { 1 } = 1 $时，y = 3 ，当$x _ { 2 } = - 1 $时，y = 3 ，此时点P 的坐标为( 1 , 3 ) ，( - 1 , 3 ) ．当$\odot P $与坐标轴相切时，则点P 的坐标为$( \sqrt { 3 } , 1 ) $或$( - \sqrt { 3 } , 1 ) $或$( \sqrt { 5 } , - 1 ) $或$( - \sqrt { 5 } , - 1 ) $或( 1 , 3 ) 或( - 1 , 3 ) ．