《2025年名师帮同步学案九年级数学全一册人教版》

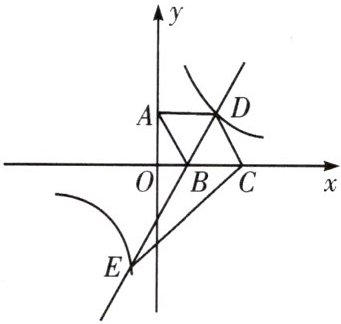
7. (例1) 如图所示, 四边形$ABCD$是菱形, 边$BC$在$x$轴上, 点$A(0,4)$, 点$B(3,0)$, 双曲线$y=\frac {k}{x}$与直线$BD$交于点$D$, 点$E$.
(1) 求$k$的值;
(2) 求直线$BD$的解析式;
(3) 求$\triangle CDE$的面积.

答案：
解:
(1)$\because$点$A(0,4)$，点$B(3,0)$，$\therefore OA=4$，$OB=3$。
由勾股定理得$AB=5$。
如图，过点$D$作$DF⊥x$轴于点$F$，则$∠AOB=∠DFC=90°$。

$\because$四边形$ABCD$是菱形，
$\therefore AB=BC=CD=AD=5$，$AD// BC$。
$\therefore AO=DF=4$。
$\because AD// BC$，$AO⊥OB$，$DF⊥x$轴，
$\therefore ∠DAO=∠AOF=∠DFO=90°$。
$\therefore$四边形$AOFD$是矩形。
$\therefore AD=OF=5$。
$\therefore$点$D$的坐标为$(5,4)$，代入$y=\frac{k}{x}$，得$k=5×4=20$。
(2)设直线$BD$的解析式为$y=ax+b(a≠0)$，把点$B(3,0)$，$D(5,4)$代入$y=ax+b$，得
$\begin{cases}3a+b=0\\5a+b=4\end{cases}$
$\therefore a=2$，$b=−6$。
$\therefore$直线$BD$的解析式是$y=2x−6$。
(3)由
(1)知$k=20$，
$\therefore y=\frac{20}{x}$。
联立方程组$\begin{cases}y=\frac{20}{x}\\y=2x−6\end{cases}$，得$\begin{cases}x_1=5\\y_1=4\end{cases}$或$\begin{cases}x_2=-2\\y_2=-10\end{cases}$。
$\because$点$D$的坐标为$(5,4)$，
$\therefore$点$E$的坐标为$(-2,-10)$。
$\because BC=5$，
$\therefore\triangle CDE$的面积为$S_{\triangle BCD}+S_{\triangle CBE}=\frac{1}{2}×5×4+\frac{1}{2}×5×10=35$。