第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
9.(例5)如图1,AB是$\odot O$的直径,AD平分$∠BAC$,连接OD,交BC于点E;
(1)求证:$\widehat {CD}=\widehat {BD},OD⊥BC,OE=\frac {1}{2}AC$且$OE// AC;$
(2)求证:$∠BAD=∠CAD=∠ADO;$
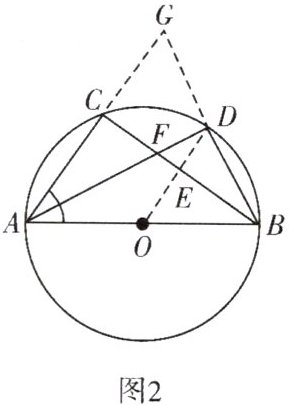
(3)如图2,分别延长AC,BD交于点G,若$AB=AG$.求证:$BD=DG;$
(4)若$∠ABC=30^{\circ }$时,求证:$AB+AC=\sqrt {3}AD;$
(5)若$AB=13,AC=5$,求AD的长.
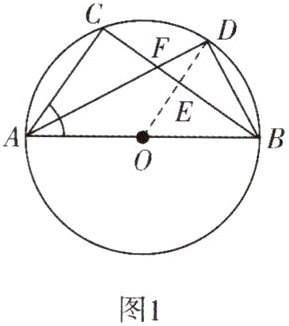
(1)求证:$\widehat {CD}=\widehat {BD},OD⊥BC,OE=\frac {1}{2}AC$且$OE// AC;$
(2)求证:$∠BAD=∠CAD=∠ADO;$
(3)如图2,分别延长AC,BD交于点G,若$AB=AG$.求证:$BD=DG;$
(4)若$∠ABC=30^{\circ }$时,求证:$AB+AC=\sqrt {3}AD;$
(5)若$AB=13,AC=5$,求AD的长.


答案:
$(1)$ 证明
- 证明$\widehat{CD}=\widehat{BD}$:
因为$AD$平分$\angle BAC$,所以$\angle BAD = \angle CAD$。
根据在同圆或等圆中,相等的圆周角所对的弧相等,可得$\widehat{CD}=\widehat{BD}$。
证明$OD\perp BC$:
连接$OC$,$OB$,因为$\widehat{CD}=\widehat{BD}$,$OC = OB$(半径相等),所以$OD\perp BC$(垂径定理的推论:平分弧的直径垂直平分弧所对的弦)。
证明$OE=\frac{1}{2}AC$且$OE// AC$:
因为$O$是$AB$中点,$OD\perp BC$,所以$E$是$BC$中点(垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,这里可推出$E$为$BC$中点)。
根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,在$\triangle ABC$中,$O$是$AB$中点,$E$是$BC$中点,所以$OE=\frac{1}{2}AC$且$OE// AC$。
$(2)$ 证明
因为$OA = OD$(半径相等),所以$\angle BAD=\angle ADO$(等边对等角)。
又因为$AD$平分$\angle BAC$,所以$\angle BAD = \angle CAD$。
所以$\angle BAD=\angle CAD=\angle ADO$。
$(3)$ 证明
连接$AD$,因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$(直径所对的圆周角是直角),即$AD\perp BG$。
又因为$AB = AG$,根据等腰三角形三线合一(等腰三角形底边上的高、底边上的中线、顶角平分线互相重合),所以$BD = DG$。
$(4)$ 证明
连接$BD$,因为$AB$是$\odot O$的直径,所以$\angle ADB=\angle ACB = 90^{\circ}$。
已知$\angle ABC = 30^{\circ}$,则$\angle BAC=60^{\circ}$,因为$AD$平分$\angle BAC$,所以$\angle BAD=\angle CAD = 30^{\circ}$。
设$BD=x$,在$Rt\triangle ABD$中,$AB = 2x$($30^{\circ}$所对直角边是斜边的一半),$AD=\sqrt{3}x$(勾股定理:$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$)。
在$Rt\triangle ABC$中,$AC=x$($\angle ABC = 30^{\circ}$,$AC=\frac{1}{2}AB$),所以$AB + AC=2x+x=3x$,$\sqrt{3}AD=\sqrt{3}×\sqrt{3}x = 3x$。
所以$AB + AC=\sqrt{3}AD$。
$(5)$ 解
连接$BC$,$BD$,因为$AB$是$\odot O$的直径,所以$\angle ACB=\angle ADB = 90^{\circ}$。
在$Rt\triangle ABC$中,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{13^{2}-5^{2}} = 12$。
由$(1)$知$OE=\frac{1}{2}AC=\frac{5}{2}$,$BE=\frac{1}{2}BC = 6$,$OB=\frac{1}{2}AB=\frac{13}{2}$。
则$DE=OD - OE=OB - OE=\frac{13}{2}-\frac{5}{2}=4$。
在$Rt\triangle BDE$中,$BD=\sqrt{BE^{2}+DE^{2}}=\sqrt{6^{2}+4^{2}} = 2\sqrt{13}$。
在$Rt\triangle ABD$中,$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{13^{2}-(2\sqrt{13})^{2}}=\sqrt{169 - 52}=\sqrt{117}=3\sqrt{13}$。
综上,$(1)$、$(2)$、$(3)$、$(4)$得证,$(5)$中$AD$的长为$\boldsymbol{3\sqrt{13}}$。
- 证明$\widehat{CD}=\widehat{BD}$:
因为$AD$平分$\angle BAC$,所以$\angle BAD = \angle CAD$。
根据在同圆或等圆中,相等的圆周角所对的弧相等,可得$\widehat{CD}=\widehat{BD}$。
证明$OD\perp BC$:
连接$OC$,$OB$,因为$\widehat{CD}=\widehat{BD}$,$OC = OB$(半径相等),所以$OD\perp BC$(垂径定理的推论:平分弧的直径垂直平分弧所对的弦)。
证明$OE=\frac{1}{2}AC$且$OE// AC$:
因为$O$是$AB$中点,$OD\perp BC$,所以$E$是$BC$中点(垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,这里可推出$E$为$BC$中点)。
根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,在$\triangle ABC$中,$O$是$AB$中点,$E$是$BC$中点,所以$OE=\frac{1}{2}AC$且$OE// AC$。
$(2)$ 证明
因为$OA = OD$(半径相等),所以$\angle BAD=\angle ADO$(等边对等角)。
又因为$AD$平分$\angle BAC$,所以$\angle BAD = \angle CAD$。
所以$\angle BAD=\angle CAD=\angle ADO$。
$(3)$ 证明
连接$AD$,因为$AB$是$\odot O$的直径,所以$\angle ADB = 90^{\circ}$(直径所对的圆周角是直角),即$AD\perp BG$。
又因为$AB = AG$,根据等腰三角形三线合一(等腰三角形底边上的高、底边上的中线、顶角平分线互相重合),所以$BD = DG$。
$(4)$ 证明
连接$BD$,因为$AB$是$\odot O$的直径,所以$\angle ADB=\angle ACB = 90^{\circ}$。
已知$\angle ABC = 30^{\circ}$,则$\angle BAC=60^{\circ}$,因为$AD$平分$\angle BAC$,所以$\angle BAD=\angle CAD = 30^{\circ}$。
设$BD=x$,在$Rt\triangle ABD$中,$AB = 2x$($30^{\circ}$所对直角边是斜边的一半),$AD=\sqrt{3}x$(勾股定理:$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{(2x)^{2}-x^{2}}=\sqrt{3}x$)。
在$Rt\triangle ABC$中,$AC=x$($\angle ABC = 30^{\circ}$,$AC=\frac{1}{2}AB$),所以$AB + AC=2x+x=3x$,$\sqrt{3}AD=\sqrt{3}×\sqrt{3}x = 3x$。
所以$AB + AC=\sqrt{3}AD$。
$(5)$ 解
连接$BC$,$BD$,因为$AB$是$\odot O$的直径,所以$\angle ACB=\angle ADB = 90^{\circ}$。
在$Rt\triangle ABC$中,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{13^{2}-5^{2}} = 12$。
由$(1)$知$OE=\frac{1}{2}AC=\frac{5}{2}$,$BE=\frac{1}{2}BC = 6$,$OB=\frac{1}{2}AB=\frac{13}{2}$。
则$DE=OD - OE=OB - OE=\frac{13}{2}-\frac{5}{2}=4$。
在$Rt\triangle BDE$中,$BD=\sqrt{BE^{2}+DE^{2}}=\sqrt{6^{2}+4^{2}} = 2\sqrt{13}$。
在$Rt\triangle ABD$中,$AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{13^{2}-(2\sqrt{13})^{2}}=\sqrt{169 - 52}=\sqrt{117}=3\sqrt{13}$。
综上,$(1)$、$(2)$、$(3)$、$(4)$得证,$(5)$中$AD$的长为$\boldsymbol{3\sqrt{13}}$。
查看更多完整答案,请扫码查看


