第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
21.公路上行驶的汽车急刹车时,刹车距离$s(\text{m})$与时间$t(\text{s})$的函数解析式$s=20t-5t^{2}$,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行
2
$\text{s}$才能停下来,最大的滑行距离为20
$\text{m}$.
答案:
220
22.已知抛物线$y=x^{2}-mx-6m^{2}$.
(1)求证:无论$x$取何值,抛物线与$x$轴总有交点;
(2)当$m=2$时,求抛物线与坐标轴的交点坐标.
(1)求证:无论$x$取何值,抛物线与$x$轴总有交点;
(2)当$m=2$时,求抛物线与坐标轴的交点坐标.
答案:
(1)证明:
∵a=1,b=−m,c=−6m²,
∴Δ=b²−4ac=(−m)²−4×1×(−6m²)=25m²≥0.故无论x取何值抛物线与x轴总有交点;
(2)解:当m=2时,抛物线的解析式为y=x²−2x−24,
令x=0,得y=−24,
令y=0,得x²−2x−24=0,
解得x₁=6,x₂=−4,
故抛物线与y轴的交点坐标为(0,−24),与x轴的交点坐标为(6,0),(−4,0).
(1)证明:
∵a=1,b=−m,c=−6m²,
∴Δ=b²−4ac=(−m)²−4×1×(−6m²)=25m²≥0.故无论x取何值抛物线与x轴总有交点;
(2)解:当m=2时,抛物线的解析式为y=x²−2x−24,
令x=0,得y=−24,
令y=0,得x²−2x−24=0,
解得x₁=6,x₂=−4,
故抛物线与y轴的交点坐标为(0,−24),与x轴的交点坐标为(6,0),(−4,0).
23.如图,点$E$,$F$,$G$,$H$分别在菱形$ABCD$的四条边上,$BE=BF=DG=DH$,连接$EF$,$FG$,$GH$,$HE$,已知$\angle A=60^{\circ}$.
(1)求$\angle HEF$的度数;
(2)判断四边形$EFGH$的形状,并说明理由;
(3)若$AB=6$,设$AE=x$.当$x$为何值时,四边形$EFGH$的面积最大?
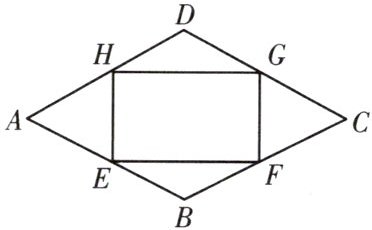
(1)求$\angle HEF$的度数;
(2)判断四边形$EFGH$的形状,并说明理由;
(3)若$AB=6$,设$AE=x$.当$x$为何值时,四边形$EFGH$的面积最大?

答案:
解:
(1)
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,
∵BE=BF=DG=DH,
∴AE=AH,
∵∠A=60°,
∴△AEH为等边三角形,∠B=120°.
∴∠AEH=60°,∠BEF=30°,
∴∠HEF=90°;
(2)四边形EFGH为矩形,理由如下:
∵DG=DH,
∴∠DHG=∠DGH=30°,
同理∠CGF=60°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(3)
∵AB=6,∠A=60°,AE=x,
∴EH=x,
则EF=$\sqrt{3}$(6−x),
则矩形EFGH的面积S=EH·EF=x·$\sqrt{3}$(6−x)= -$\sqrt{3}$x²+6$\sqrt{3}$x,
则当x = -$\frac{b}{2a}$ = -$\frac{6\sqrt{3}}{-2\sqrt{3}}$ = 3时,函数有最大值.
∴当x为3时,四边形EFGH的面积最大.
(1)
∵四边形ABCD为菱形,
∴AB=BC=CD=AD,
∵BE=BF=DG=DH,
∴AE=AH,
∵∠A=60°,
∴△AEH为等边三角形,∠B=120°.
∴∠AEH=60°,∠BEF=30°,
∴∠HEF=90°;
(2)四边形EFGH为矩形,理由如下:
∵DG=DH,
∴∠DHG=∠DGH=30°,
同理∠CGF=60°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(3)
∵AB=6,∠A=60°,AE=x,
∴EH=x,
则EF=$\sqrt{3}$(6−x),
则矩形EFGH的面积S=EH·EF=x·$\sqrt{3}$(6−x)= -$\sqrt{3}$x²+6$\sqrt{3}$x,
则当x = -$\frac{b}{2a}$ = -$\frac{6\sqrt{3}}{-2\sqrt{3}}$ = 3时,函数有最大值.
∴当x为3时,四边形EFGH的面积最大.
查看更多完整答案,请扫码查看


