《2025年名师帮同步学案九年级数学全一册人教版》

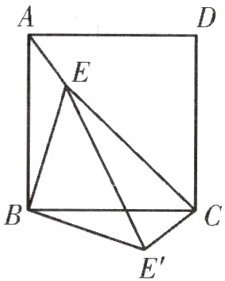
1.(例1)如图,在正方形ABCD中,$△ABE$绕点B旋转$90^{\circ }$到$△CBE'$位置,若$AE=1,BE=2,CE=3,$连接$EE'.$
(1)求证:$△BEE'$是等腰直角三角形;
(2)求$△BEE'$的周长与面积;
(3)判断$△EE'C$的形状并证明;
(4)求$∠AEB$的度数;
(5)证明:点A,E,$E'$三点共线.

答案： 证明:
(1) 由旋转得 $ BE = BE' $，旋转角 $ \angle EBE' = 90^\circ $，
$ \therefore \triangle BEE' $ 为等腰直角三角形；
(2) 解: 在 $ \text{Rt} \triangle BEE' $ 中，由勾股定理得 $ EE' = \sqrt{BE^2 + BE'^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2} $，
则 $ \triangle BEE' $ 的周长 $ C = BE + BE' + EE' = 2 + 2 + 2\sqrt{2} = 4 + 2\sqrt{2} $，
$ \triangle BEE' $ 的面积 $ S = \frac{1}{2}BE^2 = \frac{1}{2} × 2^2 = 2 $；
(3) 解: $ \triangle EE'C $ 为直角三角形，
证明: 由旋转知 $ CE' = AE = 1 $，
由
(2) 知 $ EE' = 2\sqrt{2} $，
在 $ \triangle EE'C $ 中，$ EE'^2 + CE'^2 = 8 + 1 = 9 $，$ EC^2 = 3^2 = 9 $，
$ EE'^2 + CE'^2 = EC^2 $，
由勾股定理逆定理，得
$ \triangle EE'C $ 为直角三角形，且 $ \angle EE'C = 90^\circ $；
(4) 解: $ \angle AEB = \angle BE'C $，
$ \angle ABE = \angle CBE' $，
$ \therefore \angle EBE' = 90^\circ $．
$ \because BE = 2 $，$ \therefore EE' = 2\sqrt{2} $，$ \angle BE'E = 45^\circ $．
由
(3) 知 $ \angle EE'C = 90^\circ $，
$ \therefore \angle AEB = \angle BE'C = 135^\circ $；
(5) 证明: $ \because \angle EBE' = 90^\circ $，$ \angle BE'E = 45^\circ $，
$ \therefore \angle BEE' = 180^\circ - \angle EBE' - \angle BE'E = 45^\circ $，
又 $ \because \angle AEB = 135^\circ $，
$ \therefore \angle AEB + \angle BEE' = 135^\circ + 45^\circ = 180^\circ $，
$ \therefore $ 点 $ A $，$ E $，$ E' $ 三点共线．

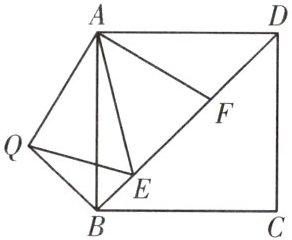
2.如图,在正方形ABCD中,E,F是对角线BD上两点,且$∠EAF=45^{\circ }$,将$△ADF$绕点A顺时针旋转$90^{\circ }$后,得到$△ABQ$,连接EQ.求证:
(1)EA是$∠QED$的平分线;
(2)$EF^{2}=BE^{2}+DF^{2}.$

答案： 证明:
(1) $ \because $ 将 $ \triangle ADF $ 绕点 $ A $ 顺时针旋转 $ 90^\circ $ 后，得到 $ \triangle ABQ $，
$ \therefore QB = DF $，$ AQ = AF $，$ \angle BAQ = \angle DAF $，
又 $ \because \angle EAF = 45^\circ $，
$ \therefore \angle DAF + \angle BAE = 45^\circ $，
$ \therefore \angle QAE = 45^\circ $，
$ \therefore \angle QAE = \angle FAE $，
在 $ \triangle AQE $ 和 $ \triangle AFE $ 中，
$ \left\{ \begin{array} { l } { AQ = AF, } \\ { \angle QAE = \angle FAE, } \\ { AE = AE, } \end{array} \right. $
$ \therefore \triangle AQE \cong \triangle AFE ( \text{SAS} ) $，
$ \therefore \angle AEQ = \angle AEF $，
$ \therefore EA $ 是 $ \angle QED $ 的平分线；
(2) 由
(1) 得 $ \triangle AQE \cong \triangle AFE $，
$ \therefore QE = EF $，
$ \because \angle QBA = \angle ADF = 45^\circ $，
$ \therefore \angle QBE = 90^\circ $．
在 $ \text{Rt} \triangle QBE $ 中，
$ QB^2 + BE^2 = QE^2 $，
则 $ EF^2 = BE^2 + DF^2 $．