《2025年名师帮同步学案九年级数学全一册人教版》

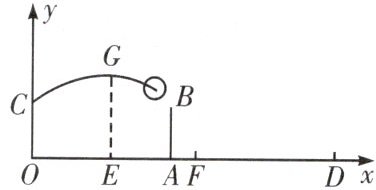
17.如图,已知排球场的长度$OD$为$18\ \text{m}$,位于球场中线处球网的高度$AB$为$2.4\ \text{m}$,一队员站在点$O$处发球,排球从点$O$的正上方$1.6\ \text{m}$的$C$点飞出,当排球运行至离点$O$的水平距离$OE$为$6\ \text{m}$时,到达最高点$G$,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为$3.4\ \text{m}$时,对方距离球网$0.4\ \text{m}$的点$F$处有一队员,他起跳后的最大高度为$3.1\ \text{m}$.问这次他是否可以拦网成功?请通过计算说明.
(2)若队员发球既要过球网,又不出边界,问排球飞行的最大高度$h$的取值范围是多少?(排球压线属于没出界)

答案： 解:
(1)根据题意知，此时抛物线的顶点G的坐标为(6,3.4)，
　设抛物线解析式为y=a(x−6)²+3.4，
　将点C(0,1.6)代入，得36a+3.4=1.6，
　解得a=−$\frac{1}{20}$，
∴排球飞行的高度y与水平距离x的函数解析式为y = -$\frac{1}{20}$(x−6)²+$\frac{17}{5}$，
　由题意当x=9.4时，y = -$\frac{1}{20}$(9.4−6)²+$\frac{17}{5}$≈2.8＜3.1，
∴这次他可以拦网成功.
(2)设抛物线解析式为y=a(x−6)²+h，将点C(0,1.6)代入，得36a+h=1.6，
　即a=$\frac{1.6−h}{36}$，
∴此时抛物线解析式为y=$\frac{1.6−h}{36}$(x−6)²+h，根据题意，得
　　$\begin{cases}\frac{9(1.6 - h)}{36}+h ＞ 2.4 \\ \frac{144(1.6 - h)}{36}+h \leq 0 \end{cases}$
　解得h＞$\frac{8}{3}$，
　答:排球飞行的最大高度h的取值范围是h＞$\frac{8}{3}$.