《2025年名师帮同步学案九年级数学全一册人教版》

9.如图,在$Rt△ABC$中,$∠BAC=90^{\circ },AB=AC$,D,E是斜边BC上两点,且$∠DAE=45^{\circ }$,将$△ADC$绕点A顺时针旋转$90^{\circ }$后得$△AFB$,连接EF,下列结论:①$△AED\cong △AEF$;②$△ABC$的面积等于四边形AFBD的面积;③$BE+DC=DE$;④$BE^{2}+CD^{2}=DE^{2}$;⑤$∠CAD=22.5^{\circ }$.其中正确的是(C)
A.①③④
B.③④⑤
C.①②④
D.①②⑤

答案： C 解析: ① 根据旋转的性质知 $ \angle CAD = \angle BAF $，$ AD = AF $，$ \because \angle BAC = 90^\circ $，$ \angle DAE = 45^\circ $，$ \therefore \angle CAD + \angle BAE = 45^\circ $，$ \therefore \angle EAF = 45^\circ $，$ \therefore \triangle AEF \cong \triangle AED $，故 ① 正确；② 易知 $ \triangle ADC \cong \triangle AFB $，$ \therefore \triangle ABC $ 的面积等于四边形 $ AFBD $ 的面积，故 ② 正确；③ 由 ① 知 $ \triangle ADE \cong \triangle AFE $，得 $ CD = BF $，$ DE = EF $．$ \therefore BE + DC = BE + BF ＞ DE = EF $，故 ③ 错误；④ $ \because AB = AC $，$ \triangle ADC $ 旋转 $ 90^\circ $ 至 $ \triangle AFB $，$ \therefore \angle BAC = 90^\circ $，$ \angle ABC = \angle ACB = 45^\circ $，又 $ \because \angle FBE = 45^\circ + 45^\circ = 90^\circ $，$ \therefore BE^2 + BF^2 = EF^2 $，又 $ \because BF = CD $，$ EF = DE $，$ \therefore BE^2 + CD^2 = DE^2 $，故 ④ 正确；$ \angle CAD = 45^\circ - \angle B $ 题目条件不足无法算出 $ \angle B $，故 ⑤ 错误；故正确的有 ①②④．故选 C．

10.问题背景:如图1,等腰直角$△ACB$中,$AC=AB,∠BAC=90^{\circ },∠CDA=45^{\circ }.$
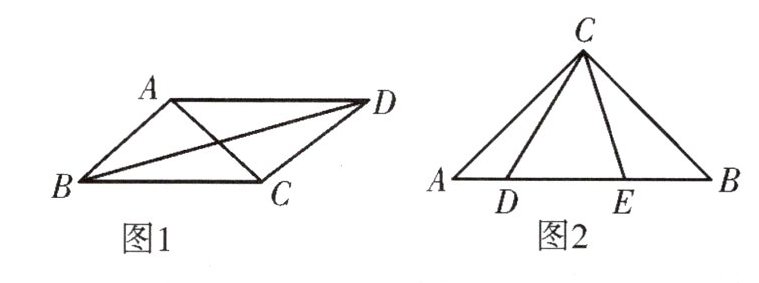
(1)画出$△ABD$绕点A逆时针旋转$90^{\circ }$后得到的$△ACE;$
(2)若$AD=4,BD=6$,求CD的长.
迁移运用:(3)如图2,等腰直角$△ACB$中,$AC=BC,∠ACB=90^{\circ }$,点D,E在线段AB上,$∠DCE=45^{\circ },∠CED=75^{\circ }$,求证:$DE=2AD.$

答案：
解:
(1) 如图所示；

(2) 如图，连接 $ DE $，
$ \because \triangle ABD \cong \triangle ACE $，
$ \therefore CE = BD = 6 $，
又 $ \because \angle EAD = 90^\circ $，
$ \therefore DE^2 = 4^2 + 4^2 = 32 $，
$ \because \angle EDA = 45^\circ $，$ \angle ADC = 45^\circ $，
$ \therefore \angle CDE = 90^\circ $．
$ \therefore CD^2 + DE^2 = CE^2 $，解得 $ CD = 2 $；
(3) 证明: 将 $ \triangle BCE $ 绕点 $ C $ 顺时针旋转 $ 90^\circ $ 到 $ \triangle ACM $，易证 $ \angle AMD = 30^\circ $，$ \angle MAD = 90^\circ $，
$ \therefore DM = 2AD $，即 $ DE = 2AD $．