《2025年名师帮同步学案九年级数学全一册人教版》

15.某商场销售一种商品,进价为每个$20$元,规定每个商品的售价不低于进价,且不高于$60$元,经调查发现,每天的销售量$y$(个)与每个商品的售价$x$(元)满足一次函数关系,其部分数据如下表所示:
|每个商品的售价$x$/元|$\cdots$|$30$|$40$|$50$|$\cdots$|
|----|----|----|----|----|----|
|每天的销售量$y$/个|$\cdots$|$100$|$80$|$60$|$\cdots$|
(1)求$y$与$x$之间的函数解析式;
(2)设商场每天获得的总利润为$\omega$(元),求$\omega$与$x$之间的函数解析式;
(3)不考虑其他因素,当每个商品的售价为多少元时,商场每天获得的总利润最大,最大总利润是多少?

答案： 解:
(1)设y与x之间的函数解析式为y=kx+b(k≠0)，代入数据，
　解得k=−2，b=160，
∴y与x之间的函数解析式是y=−2x+160(20≤x≤60);
(2)由题意可得w=(x−20)(−2x+160)=−2x²+200x−3200，
　即w与x之间的函数解析式是w=−2x²+200x−3200(20≤x≤60);
(3)
∵w=−2x²+200x−3200=−2(x−50)²+1800，(20≤x≤60)，
∴当x=50时，w取得最大值为1800，
　故当每个商品的售价为50元时，商场每天获得的总利润最大，最大总利润是1800元.

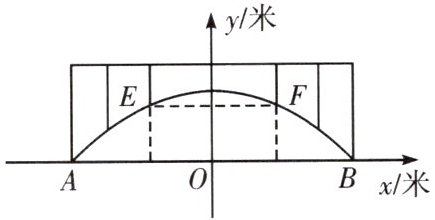
16.廊桥是我国古老的文化遗产,如图所示是一座抛物线形廊桥的示意图.已知抛物线对应的函数解析式为$y=-\frac{1}{40}x^{2}+10$.
(1)在对称轴右边$1$米处,桥拱上的点到水面$AB$的距离=9.975米;
(2)为保护廊桥的安全,在桥拱上距水面$AB$高为$8$米的点$E$,$F$处安装两盏警示灯,求这两盏灯的水平距离.

解:(2)由题意得点E，F的纵坐标为8，把y=8代入y = -$\frac{1}{40}$x²+10，
　解得x=4$\sqrt{5}$或x=−4$\sqrt{5}$，
　∴EF=|4$\sqrt{5}$−(−4$\sqrt{5}$)|=8$\sqrt{5}$(米)，
　答:这两盏灯的水平距离约为8$\sqrt{5}$米.

答案： 解:
(1)9.975
(2)由题意得点E，F的纵坐标为8，把y=8代入y = -$\frac{1}{40}$x²+10，
　解得x=4$\sqrt{5}$或x=−4$\sqrt{5}$，
∴EF=|4$\sqrt{5}$−(−4$\sqrt{5}$)|=8$\sqrt{5}$(米)，
　答:这两盏灯的水平距离约为8$\sqrt{5}$米.