第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
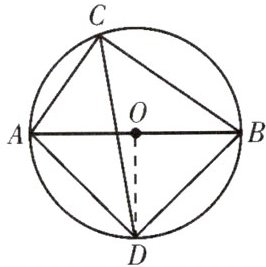
8.(例4)如图,$\odot O$的直径AB为10 cm,弦AC为6 cm,$∠ACB$的平分线交$\odot O$于点D.
(1)求BC,AD,BD的长;
(2)连接OD,求证:$\widehat {AD}=\widehat {BD},OD⊥AB,△ABD$是等腰直角三角形;
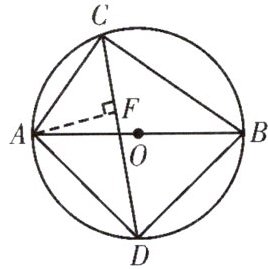
(3)过点A作$AF⊥CD$交于点F,求证:$CF=AF=\frac {\sqrt {2}}{2}AC;$
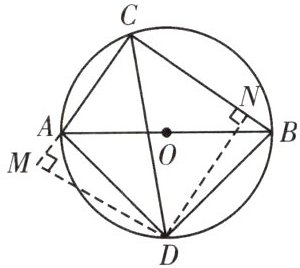
(4)过点D作$DM⊥AC$于点M,作$DN⊥BC$于点N,求证:$CA+CB=\sqrt {2}CD$(提示:证$△DMA\cong △DNB);$
(5)求证:$S_{四边形ADBC}=\frac {1}{2}CD^{2}.$

(1)求BC,AD,BD的长;
(2)连接OD,求证:$\widehat {AD}=\widehat {BD},OD⊥AB,△ABD$是等腰直角三角形;
(3)过点A作$AF⊥CD$交于点F,求证:$CF=AF=\frac {\sqrt {2}}{2}AC;$
(4)过点D作$DM⊥AC$于点M,作$DN⊥BC$于点N,求证:$CA+CB=\sqrt {2}CD$(提示:证$△DMA\cong △DNB);$
(5)求证:$S_{四边形ADBC}=\frac {1}{2}CD^{2}.$




答案:
(例 4)(1)解:$\because AB$是直径,
$\therefore \angle ACB = \angle ADB = 90 ^ { \circ },$在$\mathrm { Rt } \triangle ABC$中,$AB ^ { 2 } = AC ^ { 2 } + BC ^ { 2 },$$AB = 10 \mathrm { cm },$$AC = 6 \mathrm { cm },$
$\therefore BC ^ { 2 } = AB ^ { 2 } - AC ^ { 2 } = 10 ^ { 2 } - 6 ^ { 2 } = 64,$$\therefore BC = 8 \mathrm { cm },$
又$\because CD$平分$\angle ACB,$
$\therefore \angle ACD = \angle BCD,$$\therefore \overparen { A D } = \overparen { D B },$
$\therefore AD = BD,$又$\because $在$\mathrm { Rt } \triangle ABD$中,$AD ^ { 2 } + BD ^ { 2 } = AB ^ { 2 },$$\therefore AD ^ { 2 } + BD ^ { 2 } = 10 ^ { 2 },$
$\therefore AD = BD = 5 \sqrt { 2 } \mathrm { cm };$(2)证明:$\because AB$是直径,$\therefore \angle ACB = \angle ADB = 90 ^ { \circ },$
又$\because CD$平分$\angle ACB,$
$\therefore \angle ACD = \angle BCD = 45 ^ { \circ },$$\therefore \overparen { A D } = \overparen { D B },$
$\therefore DA = DB,$$\therefore \triangle ABD$是等腰直角三角形.
由圆周角定理得$\angle AOD = 2 \angle ACD = 90 ^ { \circ },$$\angle BOD = 2 \angle BCD = 90 ^ { \circ },$
$\therefore OD \perp AB;$(3)证明:$\because \angle ACD = \angle BCD = \frac { 1 } { 2 } \angle ACB = 45 ^ { \circ },$$\therefore $在$\mathrm { Rt } \triangle AFC$中,$CF = AF = \frac { \sqrt { 2 } } { 2 } AC;$
(4)证明:$\because DM \perp CA,$$DN \perp BC,$
$\therefore \angle DMA = \angle DNB = 90 ^ { \circ },$$\because \angle ACB = 90 ^ { \circ },$
$\therefore $四边形CMDN是矩形,$\therefore \angle MDN = 90 ^ { \circ },$
即$\angle ADN + \angle ADM = 90 ^ { \circ },$
又$\because AB$为直径,
$\therefore \angle ADB = \angle ACB = 90 ^ { \circ },$$\therefore \angle ADN + \angle BDN = 90 ^ { \circ },$
$\therefore AM = BN,$CA + CB = CM + CN + BN - AM = CM + CN,在$\mathrm { Rt } \triangle CMD$中,CD平分$\angle ACB,$$\angle ACB = 90 ^ { \circ },$
$\therefore \angle DCA = 45 ^ { \circ },$$\angle DCN = 45 ^ { \circ },$$\therefore CM = CN = \frac { \sqrt { 2 } } { 2 } CD,$
$\therefore CM + CN = \frac { \sqrt { 2 } } { 2 } CD + \frac { \sqrt { 2 } } { 2 } CD = \sqrt { 2 } CD,$即$CA + CB = \sqrt { 2 } CD;$(5)证明:由(4)证得$CM = CN = \frac { \sqrt { 2 } } { 2 } CD,$$CA + CB = \sqrt { 2 } CD,$$\therefore S _ { \text { 四边形 } A D B C } = S _ { \triangle A C D } + S _ { \triangle C D B },$
又$\because DM = DN,$
$\therefore S _ { \text { 四边形 } A D B C } = \frac { 1 } { 2 } A C \cdot M D + \frac { 1 } { 2 } B C \cdot D N = \frac { 1 } { 2 } ( A C + B C ) \cdot D N = \frac { 1 } { 2 } × \sqrt { 2 } C D \cdot \frac { \sqrt { 2 } } { 2 } C D = \frac { 1 } { 2 } C D ^ { 2 }.$
$\therefore \angle ACB = \angle ADB = 90 ^ { \circ },$在$\mathrm { Rt } \triangle ABC$中,$AB ^ { 2 } = AC ^ { 2 } + BC ^ { 2 },$$AB = 10 \mathrm { cm },$$AC = 6 \mathrm { cm },$
$\therefore BC ^ { 2 } = AB ^ { 2 } - AC ^ { 2 } = 10 ^ { 2 } - 6 ^ { 2 } = 64,$$\therefore BC = 8 \mathrm { cm },$
又$\because CD$平分$\angle ACB,$
$\therefore \angle ACD = \angle BCD,$$\therefore \overparen { A D } = \overparen { D B },$
$\therefore AD = BD,$又$\because $在$\mathrm { Rt } \triangle ABD$中,$AD ^ { 2 } + BD ^ { 2 } = AB ^ { 2 },$$\therefore AD ^ { 2 } + BD ^ { 2 } = 10 ^ { 2 },$
$\therefore AD = BD = 5 \sqrt { 2 } \mathrm { cm };$(2)证明:$\because AB$是直径,$\therefore \angle ACB = \angle ADB = 90 ^ { \circ },$
又$\because CD$平分$\angle ACB,$
$\therefore \angle ACD = \angle BCD = 45 ^ { \circ },$$\therefore \overparen { A D } = \overparen { D B },$
$\therefore DA = DB,$$\therefore \triangle ABD$是等腰直角三角形.
由圆周角定理得$\angle AOD = 2 \angle ACD = 90 ^ { \circ },$$\angle BOD = 2 \angle BCD = 90 ^ { \circ },$
$\therefore OD \perp AB;$(3)证明:$\because \angle ACD = \angle BCD = \frac { 1 } { 2 } \angle ACB = 45 ^ { \circ },$$\therefore $在$\mathrm { Rt } \triangle AFC$中,$CF = AF = \frac { \sqrt { 2 } } { 2 } AC;$
(4)证明:$\because DM \perp CA,$$DN \perp BC,$
$\therefore \angle DMA = \angle DNB = 90 ^ { \circ },$$\because \angle ACB = 90 ^ { \circ },$
$\therefore $四边形CMDN是矩形,$\therefore \angle MDN = 90 ^ { \circ },$
即$\angle ADN + \angle ADM = 90 ^ { \circ },$
又$\because AB$为直径,
$\therefore \angle ADB = \angle ACB = 90 ^ { \circ },$$\therefore \angle ADN + \angle BDN = 90 ^ { \circ },$
$\therefore AM = BN,$CA + CB = CM + CN + BN - AM = CM + CN,在$\mathrm { Rt } \triangle CMD$中,CD平分$\angle ACB,$$\angle ACB = 90 ^ { \circ },$
$\therefore \angle DCA = 45 ^ { \circ },$$\angle DCN = 45 ^ { \circ },$$\therefore CM = CN = \frac { \sqrt { 2 } } { 2 } CD,$
$\therefore CM + CN = \frac { \sqrt { 2 } } { 2 } CD + \frac { \sqrt { 2 } } { 2 } CD = \sqrt { 2 } CD,$即$CA + CB = \sqrt { 2 } CD;$(5)证明:由(4)证得$CM = CN = \frac { \sqrt { 2 } } { 2 } CD,$$CA + CB = \sqrt { 2 } CD,$$\therefore S _ { \text { 四边形 } A D B C } = S _ { \triangle A C D } + S _ { \triangle C D B },$
又$\because DM = DN,$
$\therefore S _ { \text { 四边形 } A D B C } = \frac { 1 } { 2 } A C \cdot M D + \frac { 1 } { 2 } B C \cdot D N = \frac { 1 } { 2 } ( A C + B C ) \cdot D N = \frac { 1 } { 2 } × \sqrt { 2 } C D \cdot \frac { \sqrt { 2 } } { 2 } C D = \frac { 1 } { 2 } C D ^ { 2 }.$
查看更多完整答案,请扫码查看


