第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11.「2025 北京大兴期中,」在数轴上,点 A 表示有理数 a,将点 A 向左移动 6 个单位长度后得到点 B,若点 B 表示 a 的相反数,则 a 的值为(
A. 6
B. -6
C. -3
D. 3
3
)A. 6
B. -6
C. -3
D. 3
答案:
D 因为点 A 和点 B 相距 6 个单位长度,且点 A 和点 B 表示的数互为相反数,所以点 A 和点 B 均距离原点 3 个单位长度. 又因为点 A 向左移动得到点 B,所以点 A 表示的数是正数,所以 $a=3$.
12.「2024 甘肃天水武山期中,」-2.5 与它的相反数之间的整数有(
A. 3 个
B. 4 个
C. 5 个
D. 6 个
C
)A. 3 个
B. 4 个
C. 5 个
D. 6 个
答案:
C -2.5 的相反数是 2.5,因为 -2.5 与 2.5 之间的整数有 -2,-1,0,1,2,所以 -2.5 与 2.5 之间的整数有 5 个. 故选 C.
易错警示 本题易把 0 漏掉而错选 B.
易错警示 本题易把 0 漏掉而错选 B.
13.「2025 山东济宁邹城十一中月考,」若 $-[ -(-a)]= -1$,则 a 的相反数为
-1
.
答案:
答案 -1
解析 因为 $-[-(-a)]=-a=-1$,所以 $a=1$,所以 a 的相反数为 -1.
解析 因为 $-[-(-a)]=-a=-1$,所以 $a=1$,所以 a 的相反数为 -1.
14.「2025 江苏镇江月考,」如图,数轴上的点 M,P,N,Q 分别表示四个有理数,若点 M,N 表示的有理数互为相反数,则图中表示正数的点的个数是
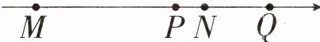
3
.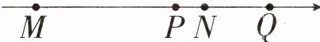
答案:
答案 3
解析 点 M,N 表示的有理数互为相反数,所以原点在 M,N 的正中间,如图,
![img alt=14]
因为位于原点右侧的点表示的数为正数,所以图中表示正数的点是 P,N,Q,共三个点.
解析 点 M,N 表示的有理数互为相反数,所以原点在 M,N 的正中间,如图,
![img alt=14]
因为位于原点右侧的点表示的数为正数,所以图中表示正数的点是 P,N,Q,共三个点.
15.「」已知 $+(-\frac{5}{3})$ 的相反数是 x,$-(+3)$ 的相反数是 y,z 的相反数是 0,则 $x + y + z$ 的相反数是____
$-\frac{14}{3}$
.
答案:
答案 $-\frac{14}{3}$
解析 因为 $+(-\frac{5}{3})=-\frac{5}{3}$,它的相反数是 $\frac{5}{3}$,所以 $x=\frac{5}{3}$. 因为 $-(+3)=-3$,它的相反数是 3,所以 $y=3$. 因为 0 的相反数是 0,所以 $z=0$,所以 $x+y+z=\frac{5}{3}+3+0=\frac{14}{3}$,所以 $x+y+z$ 的相反数是 $-\frac{14}{3}$.
解析 因为 $+(-\frac{5}{3})=-\frac{5}{3}$,它的相反数是 $\frac{5}{3}$,所以 $x=\frac{5}{3}$. 因为 $-(+3)=-3$,它的相反数是 3,所以 $y=3$. 因为 0 的相反数是 0,所以 $z=0$,所以 $x+y+z=\frac{5}{3}+3+0=\frac{14}{3}$,所以 $x+y+z$ 的相反数是 $-\frac{14}{3}$.
16.「2025 广西南宁良庆月考,」数轴上点 A 表示的数是 3,B,C 两点表示的数互为相反数,且点 B 到点 A 的距离是 2,则点 C 表示的数是
-5 或 -1
.
答案:
答案 -5 或 -1
解析 点 B 到点 A 的距离是 2,点 A 表示的数是 3,当点 B 在点 A 的右侧时,点 B 表示的数是 5;当点 B 在点 A 的左侧时,点 B 表示的数是 1. 因为 B,C 两点表示的数互为相反数,所以点 C 表示的数是 -5 或 -1.
解析 点 B 到点 A 的距离是 2,点 A 表示的数是 3,当点 B 在点 A 的右侧时,点 B 表示的数是 5;当点 B 在点 A 的左侧时,点 B 表示的数是 1. 因为 B,C 两点表示的数互为相反数,所以点 C 表示的数是 -5 或 -1.
17.「2024 广东珠海月考,」已知 2x 与 -6 互为相反数,求 x 的值.
答案:
解析 因为 2x 与 -6 互为相反数,所以 $2x=6$,所以 $x=3$,即 x 的值是 3.
18.「2025 陕西商洛月考」有理数 a,b 对应的点在数轴上的位置如图所示:
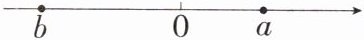
(1) 在数轴上分别用 A,B 两点表示 -a,-b.
(2) 若数 b 与 -b 对应的点相距 20 个单位长度,则数 b 与 -b 分别是
(3) 在(2)的条件下,若数 a 对应的点与数 b 对应的点相距 15 个单位长度,则数 a 与 -a 是
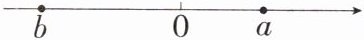
(1) 在数轴上分别用 A,B 两点表示 -a,-b.
(2) 若数 b 与 -b 对应的点相距 20 个单位长度,则数 b 与 -b 分别是
-10
、10
?(3) 在(2)的条件下,若数 a 对应的点与数 b 对应的点相距 15 个单位长度,则数 a 与 -a 是
5
、-5
?
答案:
解析
(1) 如图.
![img alt=18]
(2) 因为数 b 与 -b 对应的点相距 20 个单位长度,所以 b 和 -b 对应的点到原点的距离均为 10 个单位长度,所以数 b 是 -10,数 -b 是 10.
(3) 因为数 a 对应的点与数 b 对应的点相距 15 个单位长度,数 b 是 -10,所以数 a 是 5,则数 -a 是 -5.
(1) 如图.
![img alt=18]
(2) 因为数 b 与 -b 对应的点相距 20 个单位长度,所以 b 和 -b 对应的点到原点的距离均为 10 个单位长度,所以数 b 是 -10,数 -b 是 10.
(3) 因为数 a 对应的点与数 b 对应的点相距 15 个单位长度,数 b 是 -10,所以数 a 是 5,则数 -a 是 -5.
19. 化简下列各式,并回答问题:
$-(-9);+(-\frac{1}{5});-[ -(-4)];-[ -(+3.5)];-\{ -[ -(-5)]\};-\{ -[ -(+5)]\}$.
(1) 当 +5 前面有 2020 个负号时,化简后的结果是多少?
(2) 当 -5 前面有 2021 个负号时,化简后的结果是多少?
你能总结出什么规律?
$-(-9);+(-\frac{1}{5});-[ -(-4)];-[ -(+3.5)];-\{ -[ -(-5)]\};-\{ -[ -(+5)]\}$.
(1) 当 +5 前面有 2020 个负号时,化简后的结果是多少?
(2) 当 -5 前面有 2021 个负号时,化简后的结果是多少?
你能总结出什么规律?
答案:
解析 $-(-9)=9$,$+(-\frac{1}{5})=-\frac{1}{5}$,$-[-(-4)]=-4$,$-[-(-3.5)]=3.5$,$-\{ -[-(-5)]\} =5$,$-\{ -[-(+5)]\} =-5$.
(1) 当 +5 前面有 2020 个负号时,化简后的结果是 5.
(2) 当 -5 前面有 2021 个负号时,化简后的结果是 5.
总结规律:一个数的前面有奇数个负号时,化简后的结果等于它的相反数;有偶数个负号时,化简后的结果等于它本身.
(1) 当 +5 前面有 2020 个负号时,化简后的结果是 5.
(2) 当 -5 前面有 2021 个负号时,化简后的结果是 5.
总结规律:一个数的前面有奇数个负号时,化简后的结果等于它的相反数;有偶数个负号时,化简后的结果等于它本身.
查看更多完整答案,请扫码查看


