《2025年5年中考3年模拟七年级数学上册人教版》

1.「2025重庆江津期末」针对如图所示的月历,框中是相邻三行三列的九个数,不改变框的大小,移动框,则框中九个数的和不可能是 (D)

A.90
B.99
C.153
D.160

答案： D 设框中的九个数中最小的数为 $ x $，则其余的数分别为 $ x + 1 $，$ x + 2 $，$ x + 7 $，$ x + 8 $，$ x + 9 $，$ x + 14 $，$ x + 15 $，$ x + 16 $，则框中九个数的和为 $ 9x + 72 $，当 $ 9x + 72 = 90 $ 时，解得 $ x = 2 $，当 $ 9x + 72 = 99 $ 时，解得 $ x = 3 $，当 $ 9x + 72 = 153 $ 时，解得 $ x = 9 $，当 $ 9x + 72 = 160 $ 时，解得 $ x = \frac{88}{9} $，此时 $ x $ 不是正整数，所以框中九个数的和不可能是 160. 故选 D.

2.「2025江苏西交大苏州附中月考」在一堂充满探索与创意的“幻方”与“幻圆”活动课上,一个小组的同学挑战了一项任务:他们将1,2,3,4,5,6,7,8,9,10,11,12这12个数字填入“六角幻星”图中.这个图的魅力在于,它的每条边上的四个数字之和必须完全相同.如图,部分数字已经被填入图中的圆圈内,请你确定a的值为 (

)
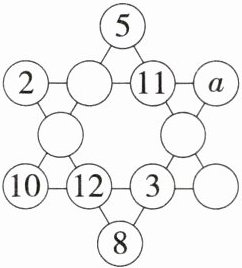
A.9
B.7
C.6
D.4

答案：
C 在图中添加字母 $ b $，$ c $，如图所示.
　　　　　　　
根据题意，得 $ 5 + 11 + b + c = 10 + 12 + 3 + c $.
即 $ 5 + 11 + b = 10 + 12 + 3 $，解得 $ b = 9 $，
所以 $ 6(a + 9 + 3 + 8) = 2×(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) $，所以 $ a = 6 $. 故选 C.

3.已知父亲和女儿现在的年龄之和是57岁,10年后,女儿的年龄是父亲年龄的$\frac {2}{5}$,设父亲现在的年龄为x岁,则可列一元一次方程为$57 - x + 10 = \frac{2}{5}(x + 10)$.

答案： 答案 $ 57 - x + 10 = \frac{2}{5}(x + 10) $
解析 父亲现在的年龄为 $ x $ 岁，则女儿现在的年龄为 $ (57 - x) $ 岁，根据 10 年后女儿的年龄是父亲年龄的 $ \frac{2}{5} $ 可列方程为 $ 57 - x + 10 = \frac{2}{5}(x + 10) $.

4.「2025湖北潜江期末改编」一个两位数个位上的数字是6,十位上的数字是x,把6与x对调,新的两位数比原两位数大36,则原两位数是______26.

答案： 答案 26
解析 因为原两位数个位上的数字是 6，十位上的数字是 $ x $，所以原两位数为 $ (10x + 6) $，把 6 与 $ x $ 对调后新的两位数为 $ (10×6 + x) $. 因为新的两位数比原两位数大 36，所以可列方程为 $ (10×6 + x) - (10x + 6) = 36 $，解得 $ x = 2 $. 所以原两位数是 26.

5.「2025甘肃兰州期末」好朋友给小亮过生日,如图,现有底面直径为16 cm,高为30 cm的圆柱形容器,里面装满了果汁,小亮要把果汁分装到底面直径为8 cm的10个小圆柱形杯子里(每个杯子都刚好装满),与好友分享,请你帮他计算杯子的高度为12cm.

答案： 解析 设杯子的高度为 $ x $ cm，
根据题意，得 $ 10π×(\frac{8}{2})^2×x = π×(\frac{16}{2})^2×30 $，
解得 $ x = 12 $. 所以杯子的高度是 12 cm.

6.「2025陕西西安蓝田期中」根据如图所示的程序框图回答问题:

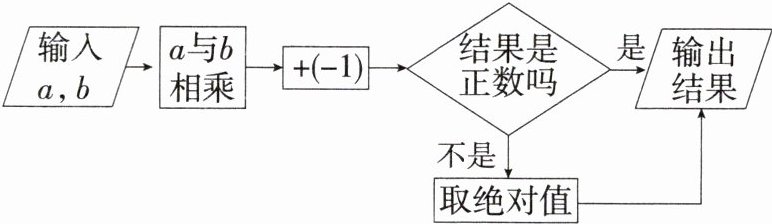
(1)当小明输入-1和-2这两个数时,输出的结果是多少?
(2)当小明输入-1和这两个数时,输出的结果是4,求被墨水污染的数.
(1)1
(2)-5或3

答案： 解析
(1) 因为 $ (-1)×(-2) + (-1) = 2 - 1 = 1 ＞ 0 $，所以当小明输入 -1 和 -2 这两个数时，输出的结果是 1.
(2) 设被墨水污染的数是 $ x $，
当 $ -1×x + (-1) ＞ 0 $ 时，$ -1×x + (-1) = 4 $，解得 $ x = -5 $；
当 $ -1×x + (-1) ＜ 0 $ 时，$ -1×x + (-1) = -4 $，解得 $ x = 3 $.
综上所述，$ x = -5 $ 或 $ x = 3 $，
所以被墨水污染的数是 -5 或 3.