《2025年5年中考3年模拟七年级数学上册人教版》

11. 学科特色 整体思想 「2024 山东济宁中考,★☆」已知 $ a ^ { 2 } - 2 b + 1 = 0 $,则 $ \frac { 4 b } { a ^ { 2 } + 1 } $ 的值是______2。

答案： 答案 2
解析 因为 $ a ^ { 2 } - 2 b + 1 = 0 $，所以 $ a ^ { 2 } + 1 = 2 b $，所以 $ \frac { 4 b } { a ^ { 2 } + 1 } = \frac { 4 b } { 2 b } = 2 $。

12. 「2025 安徽阜阳十八中期中,★☆」如图,在一块长为 $ 2 x \mathrm { m } $,宽为 $ 2 y \mathrm { m } ( y ＜ x ) $ 的长方形铁皮的四个角上,分别截去半径为 $ y \mathrm { m } $ 的圆的 $ \frac { 1 } { 4 } $。
(1) 求剩余铁皮的面积(阴影部分的面积)。
(2) 当 $ x = 4 $,$ y = 3 $ 时,剩余铁皮的面积是多少？($ \pi \approx 3.14 $,结果精确到 0.1)
(1) 剩余铁皮的面积为$4xy - \pi y^2$$\mathrm{m}^2$。
(2) 剩余铁皮的面积是19.7$\mathrm{m}^2$。

答案： 解析
(1) 根据题意可知，剩余铁皮的面积为 $ 2 x \cdot 2 y - 4 \times \frac { 1 } { 4 } \times \pi \times y ^ { 2 } = ( 4 x y - \pi y ^ { 2 } ) \mathrm { m } ^ { 2 } $。
(2) 当 $ x = 4 $，$ y = 3 $ 时，$ 4 x y - \pi y ^ { 2 } \approx 4 \times 4 \times 3 - 3.14 \times 3 ^ { 2 } = 48 - 28.26 \approx 19.7 ( \mathrm { m } ^ { 2 } ) $。
答：剩余铁皮的面积是 $ 19.7 \mathrm { m } ^ { 2 } $。

13. 新课标 应用意识 「2025 河南周口鹿邑期中」为丰富校园体育生活,某校增设网球兴趣社团,需要采购某品牌网球训练拍 30 个,网球 $ x $ 筒 $ ( x ＞ 30 ) $。经市场调查,了解到该品牌网球拍的定价为 100 元/个,网球的定价为 20 元/筒。现甲、乙两家体育用品商店有如下优惠方案：
甲商店：买一个网球拍送一筒网球；
乙商店：网球拍与网球均按定价的 90%付款。
(1) 方案一：到甲商店购买,需要支付20x+2400元；方案二：到乙商店购买,需要支付18x+2700元。(用含 $ x $ 的代数式表示)
(2) 若 $ x = 100 $,请通过计算说明 (1) 中的两个方案中,哪个方案较为优惠。
(3) 若 $ x = 100 $,你还有比 (2) 中的方案更省钱的购买方案吗？如果有,请直接写出购买方案,并写出比 (2) 中较为优惠的方案省多少钱。

答案： 解析
(1) 方案一：到甲商店购买，买一个网球拍送一筒网球，所以需要支付 $ 30 \times 100 + 20 \times ( x - 30 ) = ( 20 x + 2400 ) $ 元；
方案二：到乙商店购买，网球拍与网球均按定价的 $ 90 \% $ 付款，所以需要支付 $ 100 \times 90 \% \times 30 + 20 \times 90 \% x = ( 18 x + 2700 ) $ 元。
故答案为 $ ( 20 x + 2400 ) $；$ ( 18 x + 2700 ) $。
(2) 当 $ x = 100 $ 时，方案一：$ 20 x + 2400 = 20 \times 100 + 2400 = 4400 $，方案二：$ 18 x + 2700 = 18 \times 100 + 2700 = 4500 $，因为 $ 4400 ＜ 4500 $，所以方案一较为优惠。
(3) 有，购买方案：先在甲商店购买 30 个网球拍，获赠 30 筒网球，然后在乙商店购买 70 筒网球，需要支付 $ 100 \times 30 + 20 \times 90 \% \times 70 = 4260 $（元），比
(2) 中较为优惠的方案省 $ 4400 - 4260 = 140 $（元）。

1. [直接代入]「2025 河北廊坊期中」若 $ x = 4 $,$ y = \frac { 1 } { 2 } $,则代数式 $ 3 x - 6 y + 4 $ 的值为(D)
A. -5
B. 1
C. 7
D. 13

答案： D 因为 $ x = 4 $，$ y = \frac { 1 } { 2 } $，所以 $ 3 x - 6 y + 4 = 3 \times 4 - 6 \times \frac { 1 } { 2 } + 4 = 12 - 3 + 4 = 13 $。故选 D。

2. [整体代入]「2025 浙江杭州月考」若长方形的周长是 10,长和宽分别是 $ m $,$ n $,则代数式 $ 6 ( m + n ) - ( m + n ) ^ { 2 } $ 的值是______5。

答案： 答案 5
解析 根据题意得，$ m + n = 10 \div 2 = 5 $，所以 $ 6 ( m + n ) - ( m + n ) ^ { 2 } = 6 \times 5 - 5 ^ { 2 } = 30 - 25 = 5 $。

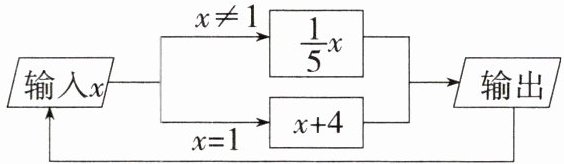
3. [循环代入] 如图所示的是一个运算程序的示意图,若开始输入 $ x $ 的值为 625,则第 2020 次输出的结果为______1。

答案： 答案 1
解析 当 $ x = 625 $ 时，$ \frac { 1 } { 5 } x = 125 $；当 $ x = 125 $ 时，$ \frac { 1 } { 5 } x = 25 $；当 $ x = 25 $ 时，$ \frac { 1 } { 5 } x = 5 $；当 $ x = 5 $ 时，$ \frac { 1 } { 5 } x = 1 $；当 $ x = 1 $ 时，$ x + 4 = 5 $；当 $ x = 5 $ 时，$ \frac { 1 } { 5 } x = 1 $；……依此类推，除前 2 次外，以 5，1 为一个循环组依次循环，$ ( 2020 - 2 ) \div 2 = 1009 $，能够整除，所以第 2020 次输出的结果是 1。

4. [先整理后代入]「2025 山东滨州期中」当 $ x = 1 $ 时,代数式 $ a x ^ { 3 } + b x + 2 $ 的值为 2024,则当 $ x = - 1 $ 时,代数式 $ a x ^ { 3 } + b x - 1 $ 的值是______-2023。

答案： 答案 - 2023
解析 因为当 $ x = 1 $ 时，代数式 $ a x ^ { 3 } + b x + 2 $ 的值为 2024，所以 $ a + b + 2 = 2024 $，所以 $ a + b = 2022 $，所以当 $ x = - 1 $ 时，$ a x ^ { 3 } + b x - 1 = - a - b - 1 = - ( a + b ) - 1 = - 2022 - 1 = - 2023 $。