第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1.「2025 湖南常德武陵期中」式子$a+2,\frac {2b}{5},2x,\frac {x+1}{3},\frac {8}{m}$中,单项式有 (
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B $\frac{2b}{5},2x$ 是单项式,有 2 个. 故选 B.
2.「2025 北京海淀期中」单项式$\frac {xy^{3}}{5}$的系数和次数分别为 (
A.$\frac {1}{5},3$
B.$\frac {1}{5},4$
C.5,3
D.5,4
B
)A.$\frac {1}{5},3$
B.$\frac {1}{5},4$
C.5,3
D.5,4
答案:
B 单项式 $\frac{xy^{3}}{5}$ 的系数与次数分别是 $\frac{1}{5},4$. 故选 B.
3.「2025 北京朝阳期中」对于多项式$x^{2}y-3xy-4$,下列说法正确的是 (
A.二次项系数是3
B.常数项是4
C.次数是3
D.项数是2
C
)A.二次项系数是3
B.常数项是4
C.次数是3
D.项数是2
答案:
C 多项式 $x^{2}y - 3xy - 4$ 的二次项系数是 $-3$,常数项是 $-4$,次数是 3,项数是 3. 故选 C.
4.下列是同类项的是 (
A.$0.2x^{2}y与0.2xy^{2}$
B.-mn与nm
C.$5^{3}与a^{3}$
D.4abc与2ac
B
)A.$0.2x^{2}y与0.2xy^{2}$
B.-mn与nm
C.$5^{3}与a^{3}$
D.4abc与2ac
答案:
B $0.2x^{2}y$ 与 $0.2xy^{2}$,相同字母 $x$ 的指数不相同,$y$ 的指数也不相同,不是同类项;$5^{3}$ 与 $a^{3}$,$5^{3}$ 不含字母,$a^{3}$ 含有字母,不是同类项;$4abc$ 与 $2ac$,$4abc$ 含有 3 个字母,$2ac$ 含有 2 个字母,不是同类项. 故选 B.
5.「2024 北京门头沟期末」下列运算正确的是 (
A.$-m-m= 0$
B.$2m+3n= 5mn$
C.$3mn-2mn= 1$
D.$m^{2}+2m^{2}= 3m^{2}$
D
)A.$-m-m= 0$
B.$2m+3n= 5mn$
C.$3mn-2mn= 1$
D.$m^{2}+2m^{2}= 3m^{2}$
答案:
D A. $-m - m = -2m$,故此选项错误;
B. $2m$ 与 $3n$ 不是同类项,不能合并,故此选项错误;
C. $3mn - 2mn = mn$,故此选项错误;
D. $m^{2} + 2m^{2} = 3m^{2}$,故此选项正确. 故选 D.
B. $2m$ 与 $3n$ 不是同类项,不能合并,故此选项错误;
C. $3mn - 2mn = mn$,故此选项错误;
D. $m^{2} + 2m^{2} = 3m^{2}$,故此选项正确. 故选 D.
6.「2025 河南商丘夏邑月考」有理数a,b,c在数轴上的对应点的位置如图所示,则化简$|a-b|-|a-c|-|c-b|$的结果为 (
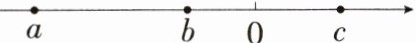
A.$a+c$
B.$a-c$
C.$2b-2c$
D.$3a-c$
C
)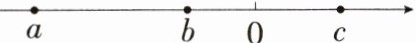
A.$a+c$
B.$a-c$
C.$2b-2c$
D.$3a-c$
答案:
C 由数轴可知,$a < b < 0 < c$,
所以 $a - b < 0$,$a - c < 0$,$c - b > 0$,
所以 $|a - b| - |a - c| - |c - b| = -(a - b) - [-(a - c)] - (c - b) = -a + b + a - c - c + b = 2b - 2c$. 故选 C.
所以 $a - b < 0$,$a - c < 0$,$c - b > 0$,
所以 $|a - b| - |a - c| - |c - b| = -(a - b) - [-(a - c)] - (c - b) = -a + b + a - c - c + b = 2b - 2c$. 故选 C.
7.「2025 山东临沂莒南期中」若关于x的多项式$mx^{2}+6x-6-(2x^{2}-4x+1)$不含二次项,则 (
A.$m= -2$
B.$m= 2$
C.$m= \frac {1}{2}$
D.$m= -\frac {1}{2}$
B
)A.$m= -2$
B.$m= 2$
C.$m= \frac {1}{2}$
D.$m= -\frac {1}{2}$
答案:
B $mx^{2} + 6x - 6 - (2x^{2} - 4x + 1) = mx^{2} + 6x - 6 - 2x^{2} + 4x - 1 = (m - 2)x^{2} + 10x - 7$,
因为关于 $x$ 的多项式 $mx^{2} + 6x - 6 - (2x^{2} - 4x + 1)$ 不含二次项,所以 $m - 2 = 0$,所以 $m = 2$. 故选 B.
因为关于 $x$ 的多项式 $mx^{2} + 6x - 6 - (2x^{2} - 4x + 1)$ 不含二次项,所以 $m - 2 = 0$,所以 $m = 2$. 故选 B.
8.「2025 山东潍坊高密月考」如图,两个正方形的面积分别为26,9,两个阴影部分的面积分别为a,b$(a>b)$,则$a-b$等于 (

A.4
B.9
C.17
D.25
C
)
A.4
B.9
C.17
D.25
答案:
C 设空白部分的面积为 $x$,由题意可得 $a + x = 26$,$b + x = 9$,所以 $(a + x) - (b + x) = 26 - 9 = 17$,所以 $a + x - b - x = 17$,所以 $a - b = 17$. 故选 C.
方法归纳 大小两个正方形的面积都包含空白部分的面积,所以设参数将空白部分的面积表示出来.
方法归纳 大小两个正方形的面积都包含空白部分的面积,所以设参数将空白部分的面积表示出来.
9.「2025 湖南怀化通道期中」在$\frac {1}{x},2x+y,\frac {1}{3}a^{2},\frac {xy}{4x},0,-23$中,整式的个数是
4
.
答案:
答案 4
解析 式子 $2x + y$,$\frac{1}{3}a^{2}$,$0$,$-23$ 符合整式的定义,是整式,故整式有 4 个.
解析 式子 $2x + y$,$\frac{1}{3}a^{2}$,$0$,$-23$ 符合整式的定义,是整式,故整式有 4 个.
10.已知单项式$3a^{m}b^{2}与-\frac {2}{3}a^{3}b^{1-n}$的和是单项式,那么$n^{m}= $
-1
.
答案:
答案 $-1$
解析 因为单项式 $3a^{m}b^{2}$ 与 $-\frac{2}{3}a^{3}b^{1 - n}$ 的和是单项式,
所以 $m = 3$,$1 - n = 2$,所以 $n = -1$,所以 $n^{m} = (-1)^{3} = -1$.
解析 因为单项式 $3a^{m}b^{2}$ 与 $-\frac{2}{3}a^{3}b^{1 - n}$ 的和是单项式,
所以 $m = 3$,$1 - n = 2$,所以 $n = -1$,所以 $n^{m} = (-1)^{3} = -1$.
11.「2024 山东德州乐陵期末」已知轮船在静水中的速度是a千米/小时,水流速度是b千米/小时,若轮船先顺水航行2小时,再逆水航行1.5小时,则轮船共航行
3.5a + 0.5b
千米.
答案:
答案 $(3.5a + 0.5b)$
解析 由题意得,轮船顺水速度为 $(a + b)$ 千米/小时,轮船顺水航行 2 小时的路程为 $2(a + b)$ 千米,轮船逆水速度为 $(a - b)$ 千米/小时,轮船逆水航行 1.5 小时的路程为 $1.5(a - b)$ 千米,所以轮船共航行 $2(a + b) + 1.5(a - b) = (3.5a + 0.5b)$ 千米.
解析 由题意得,轮船顺水速度为 $(a + b)$ 千米/小时,轮船顺水航行 2 小时的路程为 $2(a + b)$ 千米,轮船逆水速度为 $(a - b)$ 千米/小时,轮船逆水航行 1.5 小时的路程为 $1.5(a - b)$ 千米,所以轮船共航行 $2(a + b) + 1.5(a - b) = (3.5a + 0.5b)$ 千米.
12.「2024 江苏南京玄武期中」将九个代数式填入九宫格中,使得九宫格的每一横行、每一竖列以及两条对角线上的三个代数式的和都相等.已知九宫格中的部分代数式如图所示,则$M-N=$____
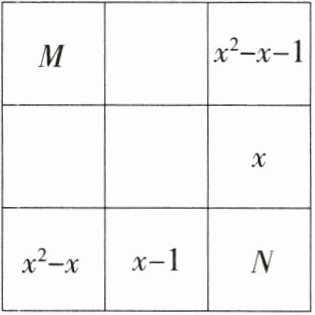
$-2x^{2} + 4x$
.(用含有x的代数式表示)
答案:
答案 $-2x^{2} + 4x$
解析 设最中间的代数式为 $P$,由题意可得 $(x^{2} - x) + (x - 1) + N = (x^{2} - x) + P + (x^{2} - x - 1)$,所以 $P = -x^{2} + 2x + N$,所以第一列中间的代数式为 $(x^{2} - x) + (x - 1) + N - (x - x^{2} + 2x + N) = 2x^{2} - 3x - 1$,因为第一列的三个代数式之和 = 第三行的三个代数式之和,所以 $M + (2x^{2} - 3x - 1) + (x^{2} - x) = (x^{2} - x) + (x - 1) + N$,化简,得 $M - N = -2x^{2} + 4x$.
解析 设最中间的代数式为 $P$,由题意可得 $(x^{2} - x) + (x - 1) + N = (x^{2} - x) + P + (x^{2} - x - 1)$,所以 $P = -x^{2} + 2x + N$,所以第一列中间的代数式为 $(x^{2} - x) + (x - 1) + N - (x - x^{2} + 2x + N) = 2x^{2} - 3x - 1$,因为第一列的三个代数式之和 = 第三行的三个代数式之和,所以 $M + (2x^{2} - 3x - 1) + (x^{2} - x) = (x^{2} - x) + (x - 1) + N$,化简,得 $M - N = -2x^{2} + 4x$.
13.「2025 陕西汉中八中期中」(8分)化简:
(1)$9a-4a+3b-5a-2b$.
(2)$2(5a^{2}-3ab+7)-(5ab-4a^{2}+7)$.
(1)$9a-4a+3b-5a-2b$.
(2)$2(5a^{2}-3ab+7)-(5ab-4a^{2}+7)$.
答案:
解析
(1) $9a - 4a + 3b - 5a - 2b$
$= (9a - 4a - 5a) + (3b - 2b) = 0 + b = b$.
(2) $2(5a^{2} - 3ab + 7) - (5ab - 4a^{2} + 7)$
$= 10a^{2} - 6ab + 14 - 5ab + 4a^{2} - 7$
$= (10a^{2} + 4a^{2}) + (-6ab - 5ab) + (14 - 7)$
$= 14a^{2} - 11ab + 7$.
(1) $9a - 4a + 3b - 5a - 2b$
$= (9a - 4a - 5a) + (3b - 2b) = 0 + b = b$.
(2) $2(5a^{2} - 3ab + 7) - (5ab - 4a^{2} + 7)$
$= 10a^{2} - 6ab + 14 - 5ab + 4a^{2} - 7$
$= (10a^{2} + 4a^{2}) + (-6ab - 5ab) + (14 - 7)$
$= 14a^{2} - 11ab + 7$.
查看更多完整答案,请扫码查看


