《2025年5年中考3年模拟七年级数学上册人教版》

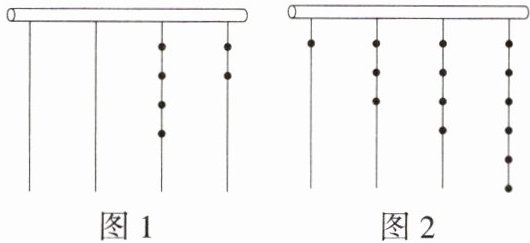
9.「2025湖北襄阳襄州期中,」在我国古代,人们通过在绳子上打结来记录数量,即“结绳记数”,一位母亲在从右到左依次排列的绳子上打结,采取满七进一的方式,用来记录孩子自出生后的天数.例如：图1表示的是孩子出生后30天时打绳结的情况(因为：$4×7^{1}+2= 30$),那么由图2可知,孩子出生后的天数是____524.

答案： 答案 524
解析 类比十进制“满十进一”，满七进一的数可以表示为“千位上的数”$×7^{3}$ + “百位上的数”$×7^{2}$ + “十位上的数”$×7^{1}$ + “个位上的数”，则$1×7^{3} + 3×7^{2} + 4×7^{1} + 6 = 524$(天). 故孩子出生后的天数是 524.

10.「2025广东东莞期中,」计算：
$|-1^{2023}|+(1-3^{2})×2-(-2)^{3}÷16$.

答案： 解析 原式$=1 + (-8)×2 - (-8)÷16 = 1 + (-16) + \frac{1}{2} = -\frac{29}{2}$.

11.「2025福建师大附中期中,」观察下列三行数,并解答后面的问题：
①$-2,4,-8,16,-32,…$；
②$1,-2,4,-8,16,…$；
③$0,-3,3,-9,15,…$.
(1)根据第①行数的规律,写出其中第n个数：____$(-2)^{n}$____.
(2)根据排列规律,分别写出上面三行数的第7个数,并计算这三个数的和.
(3)设x,y,z分别表示第①②③行数的第2024个数,求出$x+y+z$的值.

答案： 解析
(1) $-2 = (-2)^{1}$，$4 = (-2)^{2}$，$-8 = (-2)^{3}$，$16 = (-2)^{4}$，$-32 = (-2)^{5}$，……，所以第①行数的第 n 个数是$(-2)^{n}$. 故答案为$(-2)^{n}$.
(2) 观察三行数可发现，第②行数的数等于第①行数中对应位置的数的$-\frac{1}{2}$，第③行数的数等于第②行数中对应位置的数减去 1，由
(1)可得，第①行数的第 7 个数是$(-2)^{7} = - 128$，所以第②行数的第 7 个数是$-128×(-\frac{1}{2}) = 64$，第③行数的第 7 个数是$64 - 1 = 63$，所以这三个数的和是$-128 + 64 + 63 = - 1$.
(3) 由
(2)可得$x = (-2)^{2024}$，$y = (-2)^{2024}×(-\frac{1}{2}) = (-2)^{2023}$，$z = (-2)^{2023} - 1$，所以$x + y + z = (-2)^{2024} + (-2)^{2023} + (-2)^{2023} - 1 = (-2)×(-2)^{2023} + (-2)^{2023} + (-2)^{2023} - 1 = (-2)^{2023}×(-2 + 1 + 1) - 1 = - 1$，即$x + y + z$的值为$-1$.

12. 定义一种运算：$\begin{vmatrix} a&c\\ b&d\end{vmatrix} =ad-bc$,如$\begin{vmatrix} 1&-3\\ -2&0\end{vmatrix} =1×0-(-2)×(-3)= 0-6= -6$,那么当$a= (-2)^{2},b= -(-1)^{3}+1,c= -3^{2}+5,d= \frac {1}{4}-|-\frac {3}{4}|$时,求$\begin{vmatrix} a&c\\ b&d\end{vmatrix} $的值.6

答案： 解析 $a = (-2)^{2} = 4$，$b = -(-1)^{3} + 1 = 2$，$c = -3^{2} + 5 = - 9 + 5 = - 4$，$d = \frac{1}{4} - |-\frac{3}{4}| = \frac{1}{4} - \frac{3}{4} = -\frac{1}{2}$，所以$\begin{vmatrix}a&c\\b&d\end{vmatrix} = ad - bc = 4×(-\frac{1}{2}) - 2×(-4) = - 2 + 8 = 6$.

13. 观察下列解题过程.
计算：$1+5+5^{2}+5^{3}+… +5^{24}+5^{25}$.
解：设$S= 1+5+5^{2}+5^{3}+… +5^{24}+5^{25}$①,
则$5S= 5+5^{2}+5^{3}+5^{4}+… +5^{25}+5^{26}$②,
②-①,得$4S= 5^{26}-1$,
$\therefore S= \frac {5^{26}-1}{4}$.
你能用你学到的方法计算下面的题吗？
$1+3+3^{2}+3^{3}+… +3^{9}+3^{10}$.
解：设$S = 1 + 3 + 3^{2} + 3^{3} + \cdots + 3^{9} + 3^{10}$①，则$3S = 3 + 3^{2} + 3^{3} + 3^{4} + \cdots + 3^{10} + 3^{11}$②，② - ①，得$2S = 3^{11} - 1$，$\therefore S =$$\frac{3^{11} - 1}{2}$.

答案： 解析 设$S = 1 + 3 + 3^{2} + 3^{3} + \cdots + 3^{9} + 3^{10}$①，则$3S = 3 + 3^{2} + 3^{3} + 3^{4} + \cdots + 3^{10} + 3^{11}$②，② - ①，得$2S = 3^{11} - 1$，$\therefore S = \frac{3^{11} - 1}{2}$.