《2025年5年中考3年模拟七年级数学上册人教版》

12.「★☆」下列计算结果是负数的是(B)
A.$0+|-(-3)|$
B.$-1\frac {1}{2}+\frac {1}{2}$
C.$-1\frac {1}{4}+2.75$
D.$|-\frac {1}{2}|+(-\frac {1}{3})$

答案： B A. $ 0 + | -(-3) | = 0 + 3 = 3 $; B. $ -1\frac{1}{2} + \frac{1}{2} = -\left( \frac{3}{2} - \frac{1}{2} \right) = -1 $; C. $ -1\frac{1}{4} + 2.75 = +(2.75 - 1.25) = 1.5 $; D. $ \left| -\frac{1}{2} \right| + \left( -\frac{1}{3} \right) = \frac{1}{2} + \left( -\frac{1}{3} \right) = +\left( \frac{1}{2} - \frac{1}{3} \right) = \frac{1}{6} $. 故选 B.

13.「2025山东德州武城三校联考,★☆」绝对值大于2且小于6的所有负整数的和是(C)
A.-7
B.-10
C.-12
D.-14

答案： C 绝对值大于 2 且小于 6 的所有负整数为 $ -3, -4, -5 $，所以绝对值大于 2 且小于 6 的所有负整数的和为 $ -3 + (-4) + (-5) = -12 $. 故选 C.

14.「2025安徽安庆外国语学校期中,★☆」如图,直尺中2cm处对应的数轴上的数与6cm处对应的数轴上的数的和为(C)

A.-1
B.0
C.1
D.2

答案： C 直尺中 2 cm 处对应的数轴上的数为 $ -0.5 $，6 cm 处对应的数轴上的数为 1.5，所以 $ -0.5 + 1.5 = 1 $. 故选 C.

15.学科易错题特色「2025山东济南历城月考,★☆」若$|a|= 5$,$|b|= 1$,且$a\lt b$,则$a+b=$(-4或-6)
A.4
B.-6
C.-6或-4
D.6或-4

答案： C 因为 $ |a| = 5 $， $ |b| = 1 $，所以 $ a = \pm 5 $， $ b = \pm 1 $，因为 $ a ＜ b $，所以 $ a = -5 $， $ b = 1 $ 或 $ a = -5 $， $ b = -1 $，当 $ a = -5 $， $ b = 1 $ 时， $ a + b = -5 + 1 = -4 $; 当 $ a = -5 $， $ b = -1 $ 时， $ a + b = -5 + (-1) = -6 $. 综上， $ a + b $ 的值是 $ -4 $ 或 $ -6 $. 故选 C.
易错警示 本题容易漏掉“$ a = -5 $， $ b = -1 $”的情况.

16.「2025浙江金华义乌月考,★☆」小邱同学做这样一道题“计算$|(-6)+■|$”,其中“■”是被墨水污染看不清的一个数,他翻看了后面的答案,得知该题的答案是15,那么“■”表示的数是( )
A.9
B.9或-21
C.-21
D.-9或21

答案：
D $ | (-6) + | = 15 $，当 $ = 9 $ 时， $ | (-6) + 9 | = | 3 | = 3 \neq 15 $，不合题意，所以排除 A, B 选项; 当 $ = -21 $ 时， $ | (-6) + (-21) | = | -27 | = 27 \neq 15 $，不合题意，所以排除 C 选项; 当 $ = -9 $ 时， $ | (-6) + (-9) | = | -15 | = 15 $，当 $ = 21 $ 时， $ | (-6) + 21 | = | 15 | = 15 $，符合题意. 故选 D.

17.「2025甘肃武威八中期中,★☆」a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数,则$a+b+c$的值为(A)
A.-1
B.0
C.1
D.2

答案： A 因为 $ a $ 是最小的自然数， $ b $ 是最大的负整数， $ c $ 是绝对值最小的有理数，所以 $ a = 0 $， $ b = -1 $， $ c = 0 $，所以 $ a + b + c = 0 + (-1) + 0 = -1 $. 故选 A.

18.「2025山东青岛市北期末,★☆」实际测量一座山的高度时,有时需要在若干个观测点中测量两个相邻可视观测点的相对高度。如A-C为90米表示观测点A比观测点C高90米,然后用这些相对高度计算出山的高度,下表是某次测量数据的部分记录,根据这次测量的数据可得A-B是______米。

225

答案： 答案 225
解析 因为 $ A - C = 90 $ 米， $ C - D = 80 $ 米，所以 $ A - D = 90 + 80 = 170 $ (米)，因为 $ E - D = -60 $ 米，即 $ D - E = 60 $ 米，所以 $ A - E = 170 + 60 = 230 $ (米)，因为 $ F - E = 50 $ 米，即 $ E - F = -50 $ 米，所以 $ A - F = 230 + (-50) = 180 $ (米)，因为 $ G - F = -85 $ 米，即 $ F - G = 85 $ 米，所以 $ A - G = 180 + 85 = 265 $ (米)，因为 $ B - G = 40 $ 米，即 $ G - B = -40 $ 米，所以 $ A - B = 265 + (-40) = 225 $ (米).

19.新课标新考向运算能力新定义题用$[x]$表示不大于x的整数中的最大整数,如$[2.4]= 2$,$[-3.1]= -4$,请计算$[-5.2]+[4.8]= $-2。

答案： 答案 -2
解析 根据题中的新定义可知 $ [-5.2] = -6 $， $ [4.8] = 4 $，所以 $ [-5.2] + [4.8] = -6 + 4 = -2 $.

20.新课标运算能力「2024浙江金华东阳期末」如图所示的是一个二阶幻圆模型,现将-1,2,-3,4,-5,6,-7,8分别填入圆圈内,使横纵向以及内外圆圈上的4个数字之和都相等,则$a+b$的值是

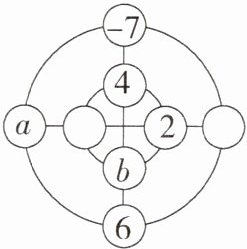
7 或 -6。

答案： 答案 7 或 -6
解析 设左边空白圆圈内的数为 $ c $，右边空白圆圈内的数为 $ d $，因为 $ (-1) + 2 + (-3) + 4 + (-5) + 6 + (-7) + 8 = 4 $，且横纵向以及内外圆圈上的 4 个数字之和都相等，所以内外圆圈上的 4 个数字之和都为 2，横纵向圆圈上的 4 个数字之和也都为 2，所以 $ (-7) + 4 + b + 6 = 2 $， $ 2 + 4 + c + b = 2 $， $ a + c + 2 + d = 2 $，所以 $ b = -1 $， $ c = -3 $， $ a + d = 3 $，当 $ a = 8 $ 时， $ d = -5 $，则 $ a + b = 8 + (-1) = 7 $; 当 $ a = -5 $ 时， $ d = 8 $，则 $ a + b = (-5) + (-1) = -6 $. 故答案为 7 或 -6.