《2025年5年中考3年模拟七年级数学上册人教版》

7.「2025河南驻马店汝南期末,★☆」如图所示的是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.设图中最大的正方形B的边长是x米.
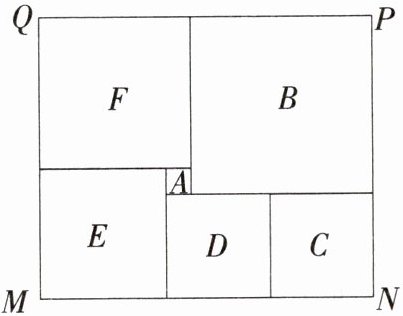
(1)请用含x的代数式分别表示出正方形F的边长= (x - 1)米,正方形E的边长= (x - 2)米,正方形C的边长= (x - 3)米.
(2)长方形相对的两边是相等的(如图中的MN= PQ),根据等量关系可求出x= 7.
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙两个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问乙队还要多少天完成? 甲、乙两个工程队各铺设多少米?

答案： 解析
(1) 由题意，得正方形 $ F $ 的边长 $ = (x - 1) $ 米，
正方形 $ E $ 的边长 $ = (x - 2) $ 米，
正方形 $ C $ 的边长 $ = \frac{x + 1}{2} $ 米（或 $ (x - 3) $ 米）.
故答案为 $ (x - 1) $ 米；$ (x - 2) $ 米；$ \frac{x + 1}{2} $ 米（或 $ (x - 3) $ 米）.
(2) 由题意，得 $ QM = (x - 1 + x - 2) $ 米，$ PN = (x + \frac{x + 1}{2}) $ 米，
因为 $ QM = PN $，所以 $ x - 1 + x - 2 = x + \frac{x + 1}{2} $，所以 $ x = 7 $.
故答案为 7.
(3) 由
(1)
(2) 可知，长方形 $ MNPQ $ 的长为 13 米，宽为 11 米，则长方形 $ MNPQ $ 的周长为 $ 2×(13 + 11) = 48 $（米）.
设乙队还要 $ y $ 天完成，由题意，得 $ (\frac{1}{10} + \frac{1}{15})×2 + \frac{1}{15}y = 1 $，
解得 $ y = 10 $. 甲队铺设 $ \frac{2}{10}×48 = 9.6 $（米），
乙队铺设 $ 48 - 9.6 = 38.4 $（米）.
答：乙队还要 10 天完成，甲队铺设 9.6 米，乙队铺设 38.4 米.

8.阅读材料:如图,在数轴上A点所表示的数为a,B点所表示的数为b,点A到点B的距离记为AB.点A到点B的距离可以用右边的点B表示的数减去左边的点A表示的数来计算,即AB= b-a.

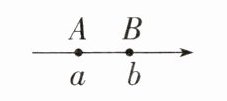
请用上面的知识解决下面的问题:
已知数轴上点A,C表示的数分别为a,c,且满足|a+7|+|c-2|= 0,点B表示的数为-3.
(1)a=-7,c=2.
(2)若在数轴上有两动点P,Q分别从A,B同时出发向右运动,点P的速度为2个单位长度/秒,点Q的速度为1个单位长度/秒,求经过多长时间P,Q两点的距离为3.
(3)在数轴上找一个点M,使得点M到点A和点C的距离之和为15,请求出点M表示

的数.

答案： 解析
(1) -7；2.
(2) 点 $ A $ 表示的数为 -7，点 $ B $ 表示的数为 -3，
设运动时间为 $ t $ s，则点 $ P $ 表示的数是 $ -7 + 2t $，点 $ Q $ 表示的数是 $ -3 + t $，
① 当点 $ P $ 在点 $ Q $ 左侧时，
$ -3 + t - (-7 + 2t) = 3 $，解得 $ t = 1 $；
② 当点 $ P $ 在点 $ Q $ 右侧时，
$ -7 + 2t - (-3 + t) = 3 $，解得 $ t = 7 $，
所以经过 1 s 或 7 s，$ P $，$ Q $ 两点的距离为 3.
(3) 由
(1) 可知，点 $ A $ 表示的数是 -7，点 $ C $ 表示的数是 2，设点 $ M $ 表示的数为 $ m $，易知分两种情况：
① 当点 $ M $ 在点 $ A $ 的左侧时，
$ MA = -7 - m $，$ MC = 2 - m $，
则 $ -7 - m + 2 - m = 15 $，解得 $ m = -10 $；
② 当点 $ M $ 在点 $ C $ 的右侧时，$ MA = m - (-7) $，$ MC = m - 2 $，
则 $ m - (-7) + m - 2 = 15 $，解得 $ m = 5 $.
综上，点 $ M $ 表示的数是 -10 或 5.