第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9.「2025 江苏南京秦淮期末」如图,把图形绕着给定的直线旋转一周后形成的几何体是(


D
)

答案:
D 将图形绕给定直线旋转一周形成一个空心的圆柱体.故选D.
10.新中华优秀传统文化「2025 四川成都锦江期末,★☆」传统竹编工艺有着悠久的历史和深刻的文化内涵,是中华民族的智慧结晶.如图,将给定的图形绕直线旋转一周得到的几何体与下列竹编工艺品的形状最为近似的是(


A
)

答案:
A 将给定的图形绕直线旋转一周得到的几何体中间细,两头一样粗.故选A.
11.「2025 山东泰安岱岳期中,★☆」如图所示的$Rt△ABC$绕直角边AC所在直线旋转一周,所得的几何体从正面看到的形状图是(
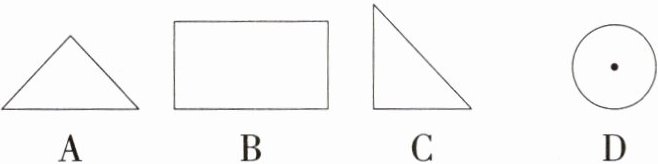
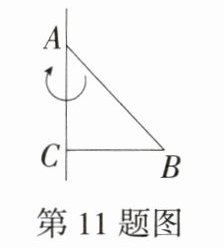
A
)

答案:
A 将Rt△ABC绕直角边AC所在直线旋转一周,所得几何体是圆锥,从正面看圆锥得到的形状图是等腰三角形,故选A.
12.教材变式「2025 河北邯郸临漳期中,★☆」如图,小军和小红分别以直角梯形的上底和下底所在的直线为轴,将梯形旋转一周,得到了甲、乙两个立体图形.
小军:我们旋转的平面图形是完全一样的,所以旋转后得到的两个立体图形的体积相等.
小红:我不同意你的看法,我认为甲、乙两个立体图形的体积不相等.

(1)你同意
(2)甲、乙两个立体图形的体积比是多少?
小军:我们旋转的平面图形是完全一样的,所以旋转后得到的两个立体图形的体积相等.
小红:我不同意你的看法,我认为甲、乙两个立体图形的体积不相等.

(1)你同意
小红
的说法.(2)甲、乙两个立体图形的体积比是多少?
5:4
答案:
解析
(1)我同意小红的说法.
理由:甲的体积$=π×3^{2}×6-\frac {1}{3}π×3^{2}×(6-3)=45π(cm^{3})$
乙的体积$=π×3^{2}×3+\frac {1}{3}π×3^{2}×(6-3)=36π(cm^{3})$
所以甲、乙两个立体图形的体积不相等.
(2)甲的体积=45πcm³,乙的体积=36πcm³,所以甲、乙两个立体图形的体积比=45π:36π=5:4.
(1)我同意小红的说法.
理由:甲的体积$=π×3^{2}×6-\frac {1}{3}π×3^{2}×(6-3)=45π(cm^{3})$
乙的体积$=π×3^{2}×3+\frac {1}{3}π×3^{2}×(6-3)=36π(cm^{3})$
所以甲、乙两个立体图形的体积不相等.
(2)甲的体积=45πcm³,乙的体积=36πcm³,所以甲、乙两个立体图形的体积比=45π:36π=5:4.
13.新空间观念已知长方形的长为4 cm,宽为3 cm,将其绕它的一边所在的直线旋转一周,得到一个立体图形,则该立体图形的体积为
36πcm³或48πcm³
.(结果保留π)
答案:
答案 36πcm³或48πcm³
解析 以4cm的边所在直线为轴,旋转一周所得到的是底面半径为3cm,高为4cm的圆柱,因此体积为$π×3^{2}×4=36π(cm^{3})$;以3cm的边所在直线为轴,旋转一周所得到的是底面半径为4cm,高为3cm的圆柱,因此体积为$π×4^{2}×3=48π(cm^{3})$.综上,该立体图形的体积为36πcm³或48πcm³.
解析 以4cm的边所在直线为轴,旋转一周所得到的是底面半径为3cm,高为4cm的圆柱,因此体积为$π×3^{2}×4=36π(cm^{3})$;以3cm的边所在直线为轴,旋转一周所得到的是底面半径为4cm,高为3cm的圆柱,因此体积为$π×4^{2}×3=48π(cm^{3})$.综上,该立体图形的体积为36πcm³或48πcm³.
14.新抽象能力欧拉是世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V、棱数E、面数F之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
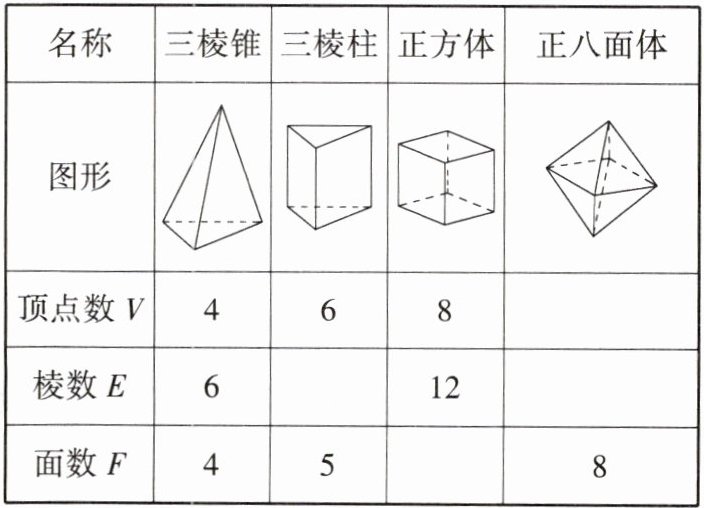
(2)分析表中的数据,你能发现V,E,F之间有什么关系吗? 请写出关系式:____.
(1)观察下列多面体,并把下表补充完整:

(2)分析表中的数据,你能发现V,E,F之间有什么关系吗? 请写出关系式:____.
答案:
解析
(1)填表如下.

(2)因为4+4−6=2,6+5−9=2,8+6−12=2,6+8−12=2,……,所以V+F−E=2.
故答案为V+F−E=2.
解析
(1)填表如下.

(2)因为4+4−6=2,6+5−9=2,8+6−12=2,6+8−12=2,……,所以V+F−E=2.
故答案为V+F−E=2.
查看更多完整答案,请扫码查看


