2025年小学毕业考试试卷精编数学徐州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小学毕业考试试卷精编数学徐州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
27. “中国天眼”是目前世界上最大口径的射电望远镜,其口径是曾经为世界上最大单口径射电望远镜——美国阿雷西博望远镜口径的$\frac{10}{7}$。已知“中国天眼”比美国阿雷西博望远镜的口径大 150 米。“中国天眼”和美国阿雷西博望远镜的口径分别是多少米? (先在线段图中将条件和问题补充完整,再列式计算)(5 分)


答案:
(线段图补充:美国阿雷西博望远镜画7段,标注“?米”;“中国天眼”画10段,与美国阿雷西博望远镜对齐,多出的3段标注“150米”,整体标注“?米”)
150÷(10-7)=50(米)
美国阿雷西博望远镜:50×7=350(米)
“中国天眼”:50×10=500(米)
答:“中国天眼”口径500米,美国阿雷西博望远镜口径350米。
150÷(10-7)=50(米)
美国阿雷西博望远镜:50×7=350(米)
“中国天眼”:50×10=500(米)
答:“中国天眼”口径500米,美国阿雷西博望远镜口径350米。
28. 小明全家 5 人在火锅店用餐,人均消费 85 元。该火锅店推出两种优惠方式。
方式一:在某平台购买 70 元抵 100 元的抵用券,不满 100 元的部分按实际支付。(如消费 368 元,300 元可以用抵用券,其余 68 元不享受优惠)
方式二:店内支付享受八折优惠。
通过计算说明他们选择哪种优惠方式更划算。(4 分)
方式一:在某平台购买 70 元抵 100 元的抵用券,不满 100 元的部分按实际支付。(如消费 368 元,300 元可以用抵用券,其余 68 元不享受优惠)
方式二:店内支付享受八折优惠。
通过计算说明他们选择哪种优惠方式更划算。(4 分)
答案:
解析:本题考查的是通过简单的四则运算解决实际问题。
方式一:
首先计算总消费金额:
$5 × 85 = 425$(元),
然后计算可以使用的抵用券数量:
$425 ÷ 100 = 4.25$,
因为只有每满100元才能使用一张抵用券,所以实际可以使用4张抵用券。
使用抵用券后的支付金额:
$4 × 70 + (425 - 4 × 100) = 280 + 25 = 305$(元),
方式二:
直接计算打折后的金额:
$425 × 0.8 = 340$(元),
最后比较两种方式的支付金额:
因为$305 \lt 340$,
所以方式一更划算。
答:他们选择方式一更划算。
方式一:
首先计算总消费金额:
$5 × 85 = 425$(元),
然后计算可以使用的抵用券数量:
$425 ÷ 100 = 4.25$,
因为只有每满100元才能使用一张抵用券,所以实际可以使用4张抵用券。
使用抵用券后的支付金额:
$4 × 70 + (425 - 4 × 100) = 280 + 25 = 305$(元),
方式二:
直接计算打折后的金额:
$425 × 0.8 = 340$(元),
最后比较两种方式的支付金额:
因为$305 \lt 340$,
所以方式一更划算。
答:他们选择方式一更划算。
29. 某校课后服务共开设了足球、儿童画、京剧、象棋四门课程。为了解学生的选课情况,学校随机抽取部分学生进行问卷调查,并根据调查结果制成了统计表和统计图。
学生选课情况统计表
2024年2月
|课程名称|选课人数|
|足球|30|
|儿童画|a|
|京剧|b|
|象棋|20|
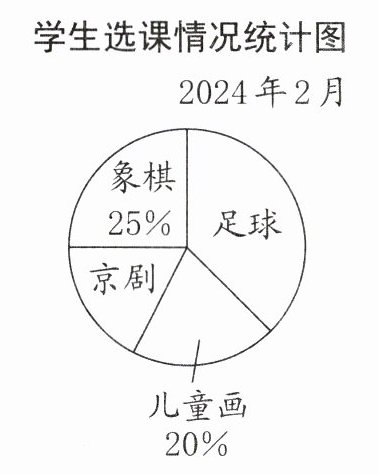
(1) 本次问卷调查共有(
(2) 统计表中,a= (
(3) 统计图中,选足球课的人数占(
(4) 如果该校共 1200 人,那么全校选足球课的大约有(
学生选课情况统计表
2024年2月
|课程名称|选课人数|
|足球|30|
|儿童画|a|
|京剧|b|
|象棋|20|

(1) 本次问卷调查共有(
80
)人参与。(1 分)(2) 统计表中,a= (
16
),b= (14
)。(2 分)(3) 统计图中,选足球课的人数占(
37.5
)%。(1 分)(4) 如果该校共 1200 人,那么全校选足球课的大约有(
450
)人。(1 分)
答案:
(1) 从统计表中可知选象棋的人数为20人,从统计图中可知选象棋的人数占总人数的$25\%$。
根据“部分量÷对应百分比 = 总量”,可得总人数为:$20÷25\%=20÷0.25 = 80$(人)。
本次问卷调查共有80人参与。
(2) 已知总人数为80人,从统计图中可知选儿童画的人数占总人数的$20\%$,选足球的人数为30人,选象棋的人数为20人,选京剧的人数占总人数的百分比为:$1 - 25\% - 20\% - \frac{30}{80}×100\%=1 - 25\% - 20\% - 37.5\% = 17.5\%$。
选儿童画的人数$a = 80×20\% = 80×0.2 = 16$(人);
选京剧的人数$b = 80×17.5\% = 80×0.175 = 14$(人)。
所以$a = 16$,$b = 14$。
(3) 选足球课的人数为30人,总人数为80人,根据“部分量÷总量×100% = 部分量占总量的百分比”,可得选足球课的人数占比为:$\frac{30}{80}×100\% = 37.5\%$。
统计图中,选足球课的人数占$37.5\%$。
(4) 已知该校共1200人,由
(3)可知选足球课的人数占总人数的$37.5\%$,则全校选足球课的大约人数为:$1200×37.5\% = 1200×0.375 = 450$(人)。
如果该校共1200人,那么全校选足球课的大约有450人。
(1) 从统计表中可知选象棋的人数为20人,从统计图中可知选象棋的人数占总人数的$25\%$。
根据“部分量÷对应百分比 = 总量”,可得总人数为:$20÷25\%=20÷0.25 = 80$(人)。
本次问卷调查共有80人参与。
(2) 已知总人数为80人,从统计图中可知选儿童画的人数占总人数的$20\%$,选足球的人数为30人,选象棋的人数为20人,选京剧的人数占总人数的百分比为:$1 - 25\% - 20\% - \frac{30}{80}×100\%=1 - 25\% - 20\% - 37.5\% = 17.5\%$。
选儿童画的人数$a = 80×20\% = 80×0.2 = 16$(人);
选京剧的人数$b = 80×17.5\% = 80×0.175 = 14$(人)。
所以$a = 16$,$b = 14$。
(3) 选足球课的人数为30人,总人数为80人,根据“部分量÷总量×100% = 部分量占总量的百分比”,可得选足球课的人数占比为:$\frac{30}{80}×100\% = 37.5\%$。
统计图中,选足球课的人数占$37.5\%$。
(4) 已知该校共1200人,由
(3)可知选足球课的人数占总人数的$37.5\%$,则全校选足球课的大约人数为:$1200×37.5\% = 1200×0.375 = 450$(人)。
如果该校共1200人,那么全校选足球课的大约有450人。
查看更多完整答案,请扫码查看


