《2025年小学毕业考试试卷精编数学徐州专版》

4. 2024年5月3日17时27分,“嫦娥六号”探测器发射升空,并飞抵距离地球约384404千米的月球。横线上的数读作(三十八万四千四百零四),省略“万”后面的尾数大约是(38)万。

答案： 解析：
题目考查大数的读法和求近似数。
读大数时，从高位读起，先读亿级，再读万级，最后读个级；读亿级和万级时按读个级的方法来读，读完亿级后加上一个“亿”字，读完万级后加上一个“万”字。
省略“万”后面的尾数求近似数时，需要看千位上数字的大小，然后用“四舍五入”法取近似数，再在数的后面写上“万”字。
答案：
三十八万四千四百零四；38

5. $\frac{3}{5}= 15:25= 0.6= 0.3÷0.5$

答案： 解析：
题目考查了比、分数和除法的关系。
首先，我们来看第一个空，需要找到一个数除以5等于0.6。设这个数为$x$，则$\frac{x}{5} = 0.6$，解得$x = 3$。
接着，我们来看第二个空，需要找到一个数，使得15与这个数的比等于0.6（或者3/5）。设这个数为$y$，则$\frac{15}{y} = 0.6$，解得：$y = \frac{15}{0.6} = 25$。
最后，我们来看第三个空，需要找到一个数除以0.5等于0.6（或者3/5）。设这个数为$z$，则$\frac{z}{0.5} = 0.6$，解得：$z = 0.6 × 0.5 = 0.3$。
答案：
3；25；0.3

6. 2024年第一季度有(91)天。
$\frac{7}{5}$升＝(1400)毫升
2500平方米＝(0.25)公顷

答案： 解析：
第一问考查不同月份的天数，季度天数的计算。
第二问考查单位换算的知识点，涉及容量单位升与毫升之间的转换。
第三问考查单位换算的知识点，涉及面积单位平方米与公顷之间的转换。
计算过程：
第一问：
2024年是闰年，2月有29天，1月有31天，3月有31天。
第一季度天数：$31 + 29 + 31 = 91(天)$。
第二问：
1升等于1000毫升。
$\frac{7}{5}$升换算为毫升：$\frac{7}{5} × 1000 = 1400(毫升)$。
第三问：
1公顷等于10000平方米。
2500平方米换算为公顷：$2500 ÷ 10000 = 0.25(公顷)$。
答案：
91；1400；0.25。

7. 在2、3、8、17、21、51这些数中,3的倍数有(3、21、51),质数有(2、3、17)。

答案： 解析：
首先，我们需要明确什么是3的倍数和质数。
3的倍数是指能被3整除的数，即该数除以3的余数为0。
质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。
接下来，我们逐一判断给出的数是否满足上述条件：
2：不是3的倍数，是质数；
3：是3的倍数，也是质数；
8：不是3的倍数，不是质数（因为8=2×4）；
17：不是3的倍数，是质数；
21：是3的倍数（21÷3=7），不是质数（因为21=3×7）；
51：是3的倍数（51÷3=17），不是质数（因为51=3×17）。
所以，3的倍数有3、21、51；质数有2、3、17。
答案：
3的倍数有(3、21、51)，质数有(2、3、17)。

8. 一幅地图的比例尺如图所示： 在这幅地图上,图上距离与实际距离的比是(1:1500000)；两地相距180千米,在这幅地图上的距离是(12)厘米。

答案： 解析：本题考查比例尺的定义及图上距离与实际距离的换算。数值比例尺是用数字的比例式或分数式表示比例尺的大小；线段比例尺是在地图上画一条线段，并注明地图上1厘米所代表实地距离多少千米。本题中地图为线段比例尺，表示图上1厘米代表实际距离15千米，根据比例尺$=$图上距离与实际距离的比，将15千米换算为以厘米为单位，即可求出数值比例尺；再将180千米换算为以厘米为单位，根据$图上距离 = 实际距离×比例尺$，可求出在这幅地图上的距离。
答案：$1:1500000$；$12$。

9. 李师傅$\frac{2}{5}小时织\frac{2}{3}$米长的毯子,照这样计算,1小时织($\frac{5}{3}$)米,$\frac{1}{5}$小时织($\frac{1}{3}$)米。

答案： $\frac{2}{3}÷\frac{2}{5}=\frac{5}{3}$（米）
$\frac{5}{3}×\frac{1}{5}=\frac{1}{3}$（米）
$\frac{5}{3}$，$\frac{1}{3}$

10. 一种压路机的前轮是圆柱形的,轮宽1.6米,直径是0.8米。前轮滚动5周,压路的面积是(20.096)平方米。

答案： 解析：
本题主要考查圆柱的侧面积公式。
将数据代入公式计算即可。
前轮滚动一周的面积即为圆柱的侧面积。
圆柱的侧面积公式为：$侧面积= \pi × 直径 × 高$
代入数值可得前轮滚动一周的面积为：
$ \pi × 0.8 × 1.6=1.28 \pi（平方米）$
前轮滚动5周的面积为：
$5 × 1.28 \pi=6.4 \pi（平方米）$
因为$\pi$取3.14，所以$6.4 \pi=6.4 × 3.14=20.096（平方米）$。
答案：20.096平方米。

11. 观察下面的直线。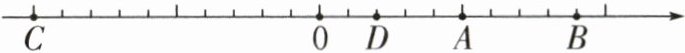
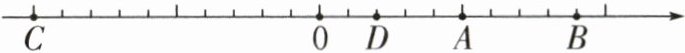
(1)若点A表示的数是1,则点B用小数表示为(1.8),点C表示的数是(-2)。
(2)若点A表示的数是$\frac{1}{3}$,则点D表示的数是($\frac{2}{15}$)。

答案： $(1)1.8 -2$　　
$(2)\frac2{15}$　　

12. 如图,两个正方形的边长分别为$a\ cm$、$b\ cm$。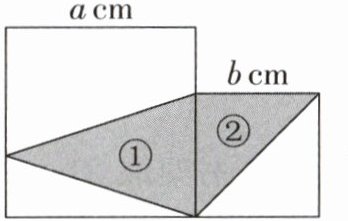
(1)用含有字母的式子表示图中涂色部分的面积是($\frac{1}{2}a(a + b)$)$cm^2$。
(2)三角形①和②的面积比是($a:b$)。

答案：
(1) $\frac{1}{2}a(a + b)$
(2) $a:b$

13. 一个15分钟的沙漏计时器,6分钟可以漏下这些沙的$\frac{2}{5}$,再漏(3)分钟后,还剩这些沙的$\frac{1}{5}$。

答案： 解析：
本题考查分数的意义和时间的计算。
第一个空，要理解6分钟是15分钟的几分之几。
由于沙漏是均匀漏沙的，所以时间比例可以代表沙漏下的比例。
6分钟是15分钟的$\frac{6}{15} = \frac{2}{5}$。
第二个空，需要找出再漏多少分钟后，沙漏剩下的沙是总量的$\frac{1}{5}$。
设再漏$x$分钟后，沙漏剩下的沙是总量的$\frac{1}{5}$。
那么，在$6+x$分钟内，沙漏漏下的沙应该是总量的$1 - \frac{1}{5} = \frac{4}{5}$。
但由于前6分钟已经漏下了$\frac{2}{5}$，所以$x$分钟内漏下的沙应该是$\frac{4}{5} - \frac{2}{5} = \frac{2}{5}$。
然而，由于沙漏是均匀的，所以$x$分钟应该是总时间的$\frac{2}{5}$对应的时间减去已经过去的6分钟所对应的时间比例部分，
即$x$应满足：
$\frac{6+x}{15} = \frac{4}{5}$
但这样解方程会比较复杂，且容易超出小学生的理解范围。
更简单的方法是，既然已经知道6分钟漏下了$\frac{2}{5}$，那么剩下的$\frac{3}{5}$中，要漏到只剩$\frac{1}{5}$，就需要漏下$\frac{2}{5}$。
由于沙漏是均匀的，所以漏下$\frac{2}{5}$的沙所需的时间也是6分钟对应的$\frac{2}{5}$的比例时间（但这里的6分钟是已经过去的时间，我们只需要考虑剩余要漏的时间）。
但实际上，我们只需要考虑剩余要漏的沙的比例是$\frac{2}{5}$，
所以时间也应该是总时间15分钟的$\frac{2}{5}$，
即$15 × \frac{2}{5} = 6$（分钟）中的“额外”部分。
不过这里的6分钟是如果从最开始算起需要的时间，
但我们已经漏了6分钟，
所以只需要再漏$15 × \frac{2}{5} - 6$分钟中“等效”的剩余时间，
这个“等效”的剩余时间其实就是总时间的$\frac{2}{5}$所对应的时间（因为沙漏是均匀的），
也就是6分钟（如果从头开始）或者理解为剩余要漏的沙的比例对应的时间。
但为了避免混淆，我们可以直接通过比例关系得出：
再漏$x$分钟后，总共漏下的沙的比例是$\frac{4}{5}$，
其中前6分钟漏了$\frac{2}{5}$，
所以$x$分钟漏了$\frac{2}{5}$，
因此$x$应该是15分钟的$\frac{2}{5}$减去已经过去的按比例算的“如果从头开始到漏完$\frac{2}{5}$所需的时间”（但这里就是6分钟，因为沙漏是均匀的），
但简化后就是$x$等于15分钟的$\frac{2}{5}$“剩余要漏的部分”（因为已经漏了6分钟，即$\frac{2}{5}$），
所以直接得出$x = 15 × \frac{2}{5} - 6$的“剩余时间”理解是不必要的，
直接$x = 15 - 15 × \frac{1}{5} - 6 = 3$分钟（这里15的$\frac{1}{5}$是剩余沙的比例对应的时间如果从头开始到漏完所有沙的时间，
但我们已经漏了到$\frac{2}{5}$，
所以只需考虑剩余到$\frac{4}{5}$的时间再减去已经过去的6分钟，
但最简单还是直接通过比例关系知道再漏$\frac{2}{5}$的沙需要的时间是总时间的$\frac{2}{5}$，
即6分钟“等效”的剩余部分，
但直接计算就是$15 - 15 × \frac{3}{5} = 6$分钟中“要漏到$\frac{4}{5}$的剩余时间”，
再减去已经漏的6分钟中的“到$\frac{2}{5}$的时间”，
结果就是3分钟）。
或者更简单地，既然6分钟漏了$\frac{2}{5}$，
那么漏完所有沙需要15分钟，
所以漏到$\frac{4}{5}$需要$15 × \frac{4}{5} = 12$分钟，
已经漏了6分钟，
所以再漏$12 - 6 = 6$分钟中的“到$\frac{4}{5}$的剩余时间部分”（但这里就是3分钟，
因为从$\frac{2}{5}$到$\frac{4}{5}$是$\frac{2}{5}$的比例，
所以时间是总时间的$\frac{2}{5}$，
即6分钟，但已经漏了6分钟到$\frac{2}{5}$，
所以只需再漏6分钟中的“剩余比例部分”，
即3分钟，因为从$\frac{2}{5}$到$\frac{4}{5}$跨越了总时间的$\frac{2}{5}$）。
但最简洁的方法还是：
总时间15分钟，漏到$\frac{1}{5}$剩余，
则已经漏了$\frac{4}{5}$，
其中前6分钟漏了$\frac{2}{5}$，
所以再漏$\frac{4}{5} - \frac{2}{5} = \frac{2}{5}$的沙所需的时间是$15 × \frac{2}{5} = 6$分钟的“剩余比例时间”（但这里的6分钟是指如果从头开始漏到$\frac{4}{5}$的时间，
已经漏了6分钟到$\frac{2}{5}$，
所以再漏的时间是$6 - 3$（这里的3是6分钟中“已经过去到$\frac{2}{5}$的时间”的一半理解，
但实际上不需要，
直接知道再漏$\frac{2}{5}$的沙是总时间的$\frac{2}{5}$，
即6分钟，但已经漏了6分钟中的“到$\frac{2}{5}$”，
所以只需3分钟即可到$\frac{4}{5}$，
因为从$\frac{2}{5}$到$\frac{4}{5}$是总时间的$\frac{2}{5}$），
所以答案是3分钟。
综合上述，
6分钟可以漏下这些沙的$\frac{2}{5}$，
再漏3分钟后，还剩这些沙的$\frac{1}{5}$。
答案：
$\frac{2}{5}$；3。

14. 已知甲、乙两个数的和是93.5,甲数的小数点向左移动一位正好等于乙数,甲、乙两个数的差是(76.5)。

答案： 设乙数为$x$，则甲数为$10x$。
$10x + x = 93.5$
$11x = 93.5$
$x = 8.5$
甲数为：$10×8.5 = 85$
甲、乙两数的差：$85 - 8.5 = 76.5$
76.5

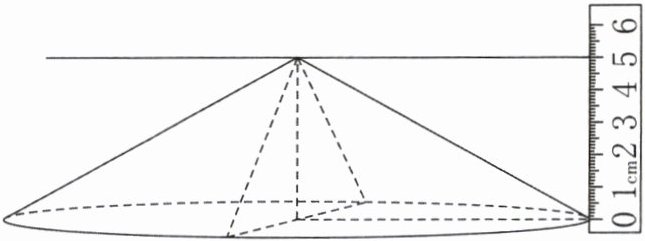
15. 如图,将圆锥沿底面直径和高切分成完全相同的两部分,表面积比原来多了90平方厘米。圆锥的底面积是(176.625)平方厘米。

答案： 由图可知圆锥的高为6厘米。
表面积增加的部分是两个完全相同的三角形，每个三角形的面积为：90÷2=45平方厘米。
三角形的底（即圆锥底面直径）为：45×2÷6=15厘米。
圆锥底面半径为：15÷2=7.5厘米。
圆锥的底面积为：3.14×7.5²=176.625平方厘米。
176.625