《2025年小学毕业考试试卷精编数学徐州专版》

18. 下面几幅图中,能表示$\frac{1}{2}×\frac{1}{3}$的含义和计算结果的是(B)。

答案： 解析：本题考查分数乘法的意义。
$\frac{1}{2}×\frac{1}{3}$表示求$\frac{1}{2}$的$\frac{1}{3}$是多少。
先把长方形平均分成2份，取其中的1份，即$\frac{1}{2}$，再把这$\frac{1}{2}$平均分成3份，取其中的1份。
A选项：把长方形平均分成6份，阴影部分占3份，表示$\frac{1}{2}$，不符合$\frac{1}{2}×\frac{1}{3}$的意义。
B选项：先把长方形平均分成2份，取其中1份（$\frac{1}{2}$），再把这$\frac{1}{2}$平均分成3份，取其中1份，符合$\frac{1}{2}×\frac{1}{3}$的意义，且$\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$，从图中可看出阴影部分占整个长方形的$\frac{1}{6}$。
C选项：把长方形平均分成4份，阴影部分占2份，表示$\frac{1}{2}$，不符合$\frac{1}{2}×\frac{1}{3}$的意义。
D选项：先把长方形平均分成3份，取其中1份（$\frac{1}{3}$），再把这$\frac{1}{3}$平均分成2份，取其中1份，表示$\frac{1}{3}×\frac{1}{2}$，虽然与$\frac{1}{2}×\frac{1}{3}$结果相同，但不符合本题$\frac{1}{2}×\frac{1}{3}$的意义。
答案：B。

19. 王阿姨去超市买苹果,每千克苹果15元。如果购买苹果的千克数用x表示,需要的元数用y表示,那么y和x是(A)。
A.成正比例的量
B.成反比例的量
C.不成比例的量
D.无法判断

答案： 解析：
题目考查了正比例和反比例的概念。
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数比值（或者说商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。
如果这两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。
在这个问题中，苹果的单价是固定的（每千克15元），所以购买苹果的总价$y$和购买的千克数$x$之间的关系可以表示为：
$y = 15x$。
这是一个正比例关系，因为$y$和$x$的比值是常数15（即单价）。
答案：A.成正比例的量。

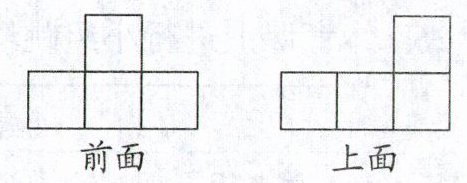
20. 若干个相同的小正方体堆在一起,从前面和上面观察,看到的图形如图所示。这些小正方体有(C)个。

A.3
B.4
C.5
D.6

答案： 解析：本题考查根据不同方向观察到的图形确定小正方体的个数。
从上面看到的图形可以确定最底层小正方体的分布情况，从前面看到的图形可以确定层数以及每列的最高层数。
从上面看，图形是两行，上面一行$3$个，下面一行$1$个靠左，说明底层有$4$个小正方体；从前面看，图形是两层，下面一层$3$个，上面一层$1$个靠左，说明一共有两层，且上层只有$1$个小正方体在左边。
所以小正方体的个数为底层的$4$个加上上层的$1$个，即$4 + 1=5$个。
答案：C。

21. 一条裤子,进价60元,以80元的价格卖出,店家收进100元,找出20元。后来发现收的100元丢失了。店家在这条裤子上实际亏了(80)元。
A.60
B.80
C.100
D.180

答案： 店家先以60元进价卖出裤子，售价80元，收100元找零20元，此时盈利80-60=20元。但后来100元丢失，损失100元。实际亏损为丢失的100元减去之前的盈利20元，即100-20=80元。
B

22. 如果下图中的①②③④⑤分别表示自然数2、4、6、8、10,那么用这样的一幅方格图,最多能表示出(B)个不同的自然数。(不考虑0)
A.22
B.23
C.24
D.25

答案： 解析：本题可通过分析方格图中每个点所代表的数值，进而找出能表示出的不同自然数的个数。
已知①②③④⑤分别表示自然数$2$、$4$、$6$、$8$、$10$，观察方格图可知，每个方格中的数是由图中黑点所对应的数字相加得到的。
方格图中一共有$3×4 = 12$个位置可以放置黑点（每个小方格看作一个位置），每个位置上的黑点代表的数值可能是$2$、$4$、$6$、$8$、$10$中的一个或者不放置黑点（代表$0$，但题目不考虑$0$）。
我们可以通过列举的方法来找出能表示出的不同自然数：
单个黑点表示的数：$2$、$4$、$6$、$8$、$10$，共$5$个。
两个黑点表示的数：
不同行不同列的组合，如$2 + 4 = 6$（与单个黑点的$6$重复，舍去）、$2+6 = 8$（重复，舍去）、$2 + 8 = 10$（重复，舍去）、$2+10 = 12$、$4 + 6 = 10$（重复，舍去）、$4+8 = 12$（重复，舍去）、$4 + 10 = 14$、$6 + 8 = 14$（重复，舍去）、$6+10 = 16$、$8 + 10 = 18$；
同行或同列的组合，比如第一行两个黑点：$2+2 = 4$（重复，舍去）等情况，去除重复后，两个黑点新得到的数有$12$、$14$、$16$、$18$，共$4$个新数。
三个黑点表示的数：
不同行不同列的组合等，如$2 + 4+6 = 12$（重复，舍去）、$2 + 4 + 8 = 14$（重复，舍去）、$2+4 + 10 = 16$（重复，舍去）、$2 + 6+8 = 16$（重复，舍去）、$2+6 + 10 = 18$（重复，舍去）、$2 + 8+10 = 20$、$4 + 6+8 = 18$（重复，舍去）、$4 + 6+10 = 20$（重复，舍去）、$4 + 8+10 = 22$、$6 + 8+10 = 24$，去除重复后，三个黑点新得到的数有$20$、$22$、$24$，共$3$个新数。
四个黑点表示的数：
如$2 + 4+6 + 8 = 20$（重复，舍去）、$2 + 4+6+10 = 22$（重复，舍去）、$2 + 4 + 8+10 = 24$（重复，舍去）、$2+6 + 8+10 = 26$、$4 + 6+8 + 10 = 28$，去除重复后，四个黑点新得到的数有$26$、$28$，共$2$个新数。
五个黑点表示的数：$2 + 4+6 + 8+10 = 30$，$1$个新数。
将所有不同数汇总：$5 + 4+3 + 2+1+10$（这里$10$是因为在列举过程中，除了上述按黑点个数分类外，还可以通过其他组合方式得到$1$到$10$这些数，$1$到$10$共$10$个数 ）$- 9$（因为$1$到$10$中$2$、$4$、$6$、$8$、$10$在单个黑点时已经算过，多算了$5$个，两个黑点组合时又重复算了一些，经分析共多算$9$个 ）$= 23$（个）。
答案：B。

23. 在左下方的方格图中画面积是16平方厘米的长方形和正方形各一个。(每个小方格表示1平方厘米)(4分)

答案： 图略
解析：本题考查长方形和正方形的面积计算。
画一个面积为$16$平方厘米的长方形：
可以选择长为$8$厘米，宽为$2$厘米的长方形。
在方格图中，从某一点开始，横向数$8$个小方格作为长，纵向数$2$个小方格作为宽，连接四个顶点，画出一个长方形。
画一个面积为$16$平方厘米的正方形：
因为正方形的面积等于边长乘边长，$4×4 = 16$，所以边长为$4$厘米。
在方格图中，从某一点开始，横向和纵向都数$4$个小方格，连接四个顶点，画出一个正方形。

24. 把右上图中的“小推车”按指定要求运动。

(1)把“小推车”先向右平移6格,再向上平移4格。分别画出两次平移后的“小推车”。(2分)
(2)如果用点A的位置(2,3)表示“小推车”的起始位置,那么第一次平移后“小推车”的位置用数对表示为(8,3),第二次平移后“小推车”的位置用数对表示为(8,7)。(2分)
(3)对照图形的运动,观察数对的变化,我发现(图形向右平移，数对中列数增加，行数不变；图形向上平移，数对中行数增加，列数不变)

答案：
(1)图略；
(2)
起始位置$A(2,3)$，根据平移规律，右加左减，上加下减。
第一次向右平移$6$格，横坐标加$6$，纵坐标不变，得到$(2 + 6,3)=(8,3)$；
第二次在第一次的基础上向上平移$4$格，横坐标不变，纵坐标加$4$，得到$(8,3 + 4)=(8,7)$。
本题应填：8；3；8；7。
(3)
通过观察图形平移前后数对的变化，发现：
图形向右平移时，数对中表示列的第一个数增加，行数不变；
图形向上平移时，数对中表示行的第二个数增加，列数不变。
所以对照图形的运动，观察数对的变化，我发现图形向右平移，数对中列数增加，行数不变；图形向上平移，数对中行数增加，列数不变。