2025年小学毕业考试试卷精编数学徐州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小学毕业考试试卷精编数学徐州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
8. 如下图(单位:厘米),下面说法正确的是(
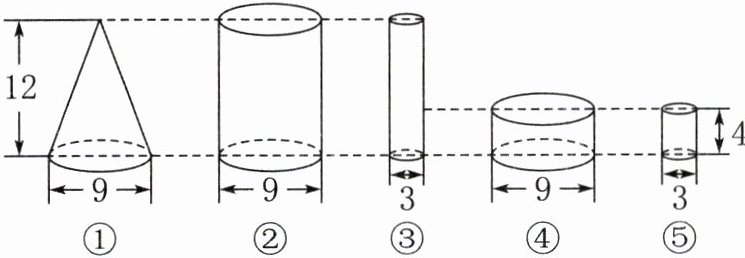
A.②号体积与①号体积的比是$1:3$
B.③号底面积是②号底面积的$\frac{1}{3}$
C.④号体积是⑤号体积的3倍
D.④号体积与①号体积相等
AD
)。
A.②号体积与①号体积的比是$1:3$
B.③号底面积是②号底面积的$\frac{1}{3}$
C.④号体积是⑤号体积的3倍
D.④号体积与①号体积相等
答案:
A. ①号体积:$\frac{1}{3}π(\frac{9}{2})^2×12 = 81π$,②号体积:$π(\frac{9}{2})^2×12 = 243π$,比为$1:3$,正确。
B. ②号底面积:$π(\frac{9}{2})^2 = \frac{81}{4}π$,③号底面积:$π(\frac{3}{2})^2 = \frac{9}{4}π$,$\frac{9}{4}π÷\frac{81}{4}π = \frac{1}{9}$,错误。
C. ④号体积:$π(\frac{9}{2})^2×4 = 81π$,⑤号体积:$π(\frac{3}{2})^2×4 = 9π$,$81π÷9π = 9$,错误。
D. ④号体积$81π$,①号体积$81π$,相等,正确。
答案:AD
B. ②号底面积:$π(\frac{9}{2})^2 = \frac{81}{4}π$,③号底面积:$π(\frac{3}{2})^2 = \frac{9}{4}π$,$\frac{9}{4}π÷\frac{81}{4}π = \frac{1}{9}$,错误。
C. ④号体积:$π(\frac{9}{2})^2×4 = 81π$,⑤号体积:$π(\frac{3}{2})^2×4 = 9π$,$81π÷9π = 9$,错误。
D. ④号体积$81π$,①号体积$81π$,相等,正确。
答案:AD
9. 如下图,有一个边长50米的等边三角形花圃,小玲想要从点M走到点N,可以(

A.向南偏西$30^{\circ}$方向走50米
B.向南偏西$60^{\circ}$方向走50米
C.向北偏东$30^{\circ}$方向走50米
D.向北偏东$60^{\circ}$方向走50米
B
)。
A.向南偏西$30^{\circ}$方向走50米
B.向南偏西$60^{\circ}$方向走50米
C.向北偏东$30^{\circ}$方向走50米
D.向北偏东$60^{\circ}$方向走50米
答案:
本题考查对方位的认识。
从图中可以看出,三角形花圃是一个等边三角形,边长为50米,点M、N、O分别为三角形的三个顶点,上方为北。
则从点M到点N,需要向南偏西$60^{\circ}$方向走50米。
故答案为B.向南偏西$60^{\circ}$方向走50米。
从图中可以看出,三角形花圃是一个等边三角形,边长为50米,点M、N、O分别为三角形的三个顶点,上方为北。
则从点M到点N,需要向南偏西$60^{\circ}$方向走50米。
故答案为B.向南偏西$60^{\circ}$方向走50米。
10. 某班女生进行仰卧起坐测试,1分钟做30个为达标。如果小红做了32个,记作"+2个",小兰做了29个,记作"-1个",那么下表中的5名女生平均每人做了(
|女生①|女生②|女生③|女生④|女生⑤|
|+3个|-7个|+15个|-6个|0个|
A.5
B.25
C.31
D.35
C
)个仰卧起坐。|女生①|女生②|女生③|女生④|女生⑤|
|+3个|-7个|+15个|-6个|0个|
A.5
B.25
C.31
D.35
答案:
首先,根据题目,达标是30个仰卧起坐,超过的记作正数,不足的记作负数。
女生①:做了$30+3=33(个)$;
女生②:做了$30-7=23(个)$;
女生③:做了$30+15=45(个)$;
女生④:做了$30-6=24(个)$;
女生⑤:做了$30+0=30(个)$。
接下来,计算5名女生做的总数:
$33+23+45+24+30=155(个)$。
然后,计算平均每人做的个数:
$155 ÷ 5=31(个)$。
所以,5名女生平均每人做了31个仰卧起坐。
答案:C.31。
女生①:做了$30+3=33(个)$;
女生②:做了$30-7=23(个)$;
女生③:做了$30+15=45(个)$;
女生④:做了$30-6=24(个)$;
女生⑤:做了$30+0=30(个)$。
接下来,计算5名女生做的总数:
$33+23+45+24+30=155(个)$。
然后,计算平均每人做的个数:
$155 ÷ 5=31(个)$。
所以,5名女生平均每人做了31个仰卧起坐。
答案:C.31。
11. 把一批书按$2:3:4或者3:2:6$的比分给三个班,都正好分完。这批书可能有(
A.90
B.99
C.100
D.110
B
)本。A.90
B.99
C.100
D.110
答案:
2+3+4=9,3+2+6=11,9和11的最小公倍数是99,选项中99符合。答案选B。
12. 如下图,有一只蚂蚁从点O出发,沿着半圆的边线爬了一圈,又回到了点O。下面可以描述蚂蚁与点O距离随时间变化情况的是图(
]

D
)。]

答案:
解析:本题考查单式折线统计图的特点及应用。
蚂蚁从点O出发,沿着半圆的边线爬了一圈,又回到了点O,说明蚂蚁与点O的距离先逐渐增大,后逐渐减小,最后为0。
A选项:距离一直均匀增大,不符合。
B选项:距离先增大后保持不变,不符合。
C选项:距离先增大后减小,但最后不为0,不符合。
D选项:距离先增大,后保持不变,再减小到0,符合。
答案:D。
蚂蚁从点O出发,沿着半圆的边线爬了一圈,又回到了点O,说明蚂蚁与点O的距离先逐渐增大,后逐渐减小,最后为0。
A选项:距离一直均匀增大,不符合。
B选项:距离先增大后保持不变,不符合。
C选项:距离先增大后减小,但最后不为0,不符合。
D选项:距离先增大,后保持不变,再减小到0,符合。
答案:D。
13. 如下图,小明准备把一根长13 cm的吸管剪成三段围成三角形。如果第一次在3 cm处剪了一刀,那么第二次在(

A.①
B.②
C.③
D.④
C
)处剪,得到的三段吸管能围成三角形。
A.①
B.②
C.③
D.④
答案:
第一次在3cm处剪断,得到一段3cm的吸管,剩余吸管长13-3=10cm。设第二次剪断位置距离0cm处为x cm(x>3),则三段吸管长度分别为3cm、(x-3)cm、(13-x)cm。
根据三角形三边关系:
1. 3 + (x-3) > 13 - x → x > 6.5
2. 3 + (13 - x) > x - 3 → x < 9.5
3. (x - 3) + (13 - x) > 3 → 10 > 3(恒成立)
综上,6.5 < x < 9.5。观察图示,①~④位置中,只有③在6.5~9.5范围内。
答案:C
根据三角形三边关系:
1. 3 + (x-3) > 13 - x → x > 6.5
2. 3 + (13 - x) > x - 3 → x < 9.5
3. (x - 3) + (13 - x) > 3 → 10 > 3(恒成立)
综上,6.5 < x < 9.5。观察图示,①~④位置中,只有③在6.5~9.5范围内。
答案:C
14. 一个圆柱的底面半径和高的比是$1:2\pi$,下面图(

A
)是这个圆柱的侧面展开图。
答案:
本题可先设出圆柱底面半径,再根据底面半径与高的关系求出高,然后结合圆柱侧面展开图的性质求出底面圆的周长,最后根据展开图的边长关系判断选项。
步骤一:设圆柱底面半径并求出高
设圆柱的底面半径为$r$,已知圆柱的底面半径和高的比是$1:2\pi$,则圆柱的高$h = 2\pi r$。
步骤二:求出底面圆的周长
根据圆的周长公式$C = 2\pi r$(其中$C$为周长,$r$为半径),可知该圆柱底面圆的周长$C = 2\pi r$。
步骤三:分析圆柱侧面展开图的边长关系
圆柱的侧面展开图是一个平行四边形(或长方形),其中一边为圆柱的高$h$,另一边为底面圆的周长$C$。
由前面计算可知$C = 2\pi r$,$h = 2\pi r$,即$C = h$。
选项$A$:平行四边形的底和高都为$a$,满足$C = h$。
选项$B$:平行四边形的邻边都为$a$,不满足$C = h$(这里$C$和$h$分别对应底和高)。
选项$C$:平行四边形的底为$2a$,邻边为$a$,不满足$C = h$。
选项$D$:长方形的长为$2a$,宽为$a$,不满足$C = h$。
所以,答案是$\boldsymbol{A}$。
步骤一:设圆柱底面半径并求出高
设圆柱的底面半径为$r$,已知圆柱的底面半径和高的比是$1:2\pi$,则圆柱的高$h = 2\pi r$。
步骤二:求出底面圆的周长
根据圆的周长公式$C = 2\pi r$(其中$C$为周长,$r$为半径),可知该圆柱底面圆的周长$C = 2\pi r$。
步骤三:分析圆柱侧面展开图的边长关系
圆柱的侧面展开图是一个平行四边形(或长方形),其中一边为圆柱的高$h$,另一边为底面圆的周长$C$。
由前面计算可知$C = 2\pi r$,$h = 2\pi r$,即$C = h$。
选项$A$:平行四边形的底和高都为$a$,满足$C = h$。
选项$B$:平行四边形的邻边都为$a$,不满足$C = h$(这里$C$和$h$分别对应底和高)。
选项$C$:平行四边形的底为$2a$,邻边为$a$,不满足$C = h$。
选项$D$:长方形的长为$2a$,宽为$a$,不满足$C = h$。
所以,答案是$\boldsymbol{A}$。
查看更多完整答案,请扫码查看


