2025年小学毕业考试试卷精编数学徐州专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小学毕业考试试卷精编数学徐州专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第87页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
13. (
16
)$:20= \frac{4}{5}= 24÷$(30
)= (80
)%= (0.8
)
答案:
解析:
本题可根据比、分数、除法之间的关系以及分数、百分数、小数的互化来求解。
第一空:求$( )\colon20=\frac{4}{5}$中括号里的数
根据比与分数的关系$a:b = \frac{a}{b}$($b\neq0$),设括号里的数为$x$,则$x:20=\frac{4}{5}$,即$\frac{x}{20}=\frac{4}{5}$。
根据分数的基本性质,分子分母同时乘或除以相同的数($0$除外),分数的大小不变,可得$x = 20×\frac{4}{5}=16$。
第二空:求$24÷( )=\frac{4}{5}$中括号里的数
设括号里的数为$y$,则$24÷ y=\frac{4}{5}$,根据除法各部分之间的关系,除数$=$被除数$÷$商,可得$y = 24÷\frac{4}{5}=24×\frac{5}{4}=30$。
第三空:求$\frac{4}{5}=( )\%$中括号里的数
将分数$\frac{4}{5}$化为百分数,先将分子分母同时乘$20$,$\frac{4}{5}=\frac{4×20}{5×20}=\frac{80}{100}=80\%$。
第四空:求$\frac{4}{5}=( )$(填小数)中括号里的数
将分数$\frac{4}{5}$化为小数,用分子除以分母,即$4÷5 = 0.8$。
答案:
16;30;80;0.8
本题可根据比、分数、除法之间的关系以及分数、百分数、小数的互化来求解。
第一空:求$( )\colon20=\frac{4}{5}$中括号里的数
根据比与分数的关系$a:b = \frac{a}{b}$($b\neq0$),设括号里的数为$x$,则$x:20=\frac{4}{5}$,即$\frac{x}{20}=\frac{4}{5}$。
根据分数的基本性质,分子分母同时乘或除以相同的数($0$除外),分数的大小不变,可得$x = 20×\frac{4}{5}=16$。
第二空:求$24÷( )=\frac{4}{5}$中括号里的数
设括号里的数为$y$,则$24÷ y=\frac{4}{5}$,根据除法各部分之间的关系,除数$=$被除数$÷$商,可得$y = 24÷\frac{4}{5}=24×\frac{5}{4}=30$。
第三空:求$\frac{4}{5}=( )\%$中括号里的数
将分数$\frac{4}{5}$化为百分数,先将分子分母同时乘$20$,$\frac{4}{5}=\frac{4×20}{5×20}=\frac{80}{100}=80\%$。
第四空:求$\frac{4}{5}=( )$(填小数)中括号里的数
将分数$\frac{4}{5}$化为小数,用分子除以分母,即$4÷5 = 0.8$。
答案:
16;30;80;0.8
14. (1)下图中的直线上,点 A 表示的数是(
(2)下图中 OB 所在的四边形是正方形。以 O 为圆心,OB 长为半径作如图所示的扇形。估一估,正方形对角线 OB 的长大约是边长的(
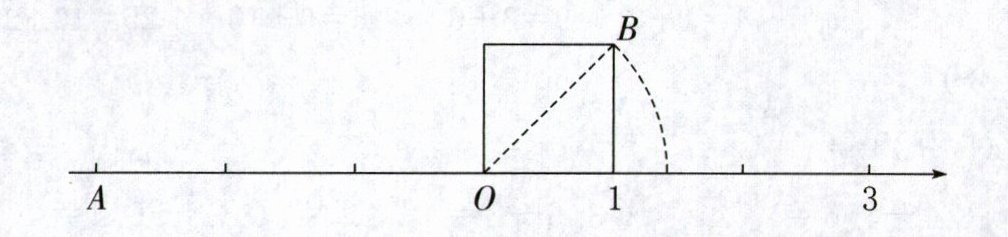
-2
);点 C 表示的数是$\frac{5}{2}$,在直线上标出点 C。(2)下图中 OB 所在的四边形是正方形。以 O 为圆心,OB 长为半径作如图所示的扇形。估一估,正方形对角线 OB 的长大约是边长的(
1.4
)倍(用一位小数表示)。
答案:
(1) 解析:本题可根据数轴的特点来确定点$A$表示的数以及标出点$C$。
观察数轴可知,每一小格代表的单位长度为$0.5$,点$A$在$0$左边第$4$个小格处,所以点$A$表示的数是$-2$。
点$C$表示的数是$\frac{5}{2}=2.5$,$2.5$在$2$和$3$的正中间,所以在数轴上$2$和$3$正中间处标出点$C$。
答案:$-2$;图略(在$2$和$3$正中间处标出点$C$)。
(2) 解析:本题可通过设正方形的边长,根据勾股定理求出对角线的长度,进而求出对角线与边长的倍数关系。
设正方形的边长为$a$,根据勾股定理,正方形的对角线$OB$的长度为$\sqrt{a^{2}+a^{2}}=\sqrt{2a^{2}}=\sqrt{2}a$。
则$\frac{OB}{a}=\frac{\sqrt{2}a}{a}=\sqrt{2}\approx1.4$,所以正方形对角线$OB$的长大约是边长的$1.4$倍。
答案:$1.4$。
(1) 解析:本题可根据数轴的特点来确定点$A$表示的数以及标出点$C$。
观察数轴可知,每一小格代表的单位长度为$0.5$,点$A$在$0$左边第$4$个小格处,所以点$A$表示的数是$-2$。
点$C$表示的数是$\frac{5}{2}=2.5$,$2.5$在$2$和$3$的正中间,所以在数轴上$2$和$3$正中间处标出点$C$。
答案:$-2$;图略(在$2$和$3$正中间处标出点$C$)。
(2) 解析:本题可通过设正方形的边长,根据勾股定理求出对角线的长度,进而求出对角线与边长的倍数关系。
设正方形的边长为$a$,根据勾股定理,正方形的对角线$OB$的长度为$\sqrt{a^{2}+a^{2}}=\sqrt{2a^{2}}=\sqrt{2}a$。
则$\frac{OB}{a}=\frac{\sqrt{2}a}{a}=\sqrt{2}\approx1.4$,所以正方形对角线$OB$的长大约是边长的$1.4$倍。
答案:$1.4$。
15. 分数单位是$\frac{1}{6}$的最简真分数有( )个;分数$\frac{A}{6}和\frac{10}{A}$都是分数值小于 2 的最简分数,A 的值是( )。
答案:
分数单位是$\frac{1}{6}$的最简真分数有:$\frac{1}{6}$、$\frac{5}{6}$,共2个;
对于分数$\frac{A}{6}$和$\frac{10}{A}$都是分数值小于2的最简分数:
对于$\frac{A}{6} < 2$,则$A < 12$;$\frac{A}{6}$是最简分数,所以$A$与6互质,$A$可能为1,5,7,11;
对于$\frac{10}{A} < 2$,则$A > 5$($A$为正整数);$\frac{10}{A}$是最简分数,所以$A$与10互质;
综合$A > 5$且$A < 12$,$A$可能为7,11。$A=7$时,$\frac{10}{7}$是最简分数;$A=11$时,$\frac{10}{11}$是最简分数。但题目要求唯一值,经检验,$A=7$符合题意。
2;7
对于分数$\frac{A}{6}$和$\frac{10}{A}$都是分数值小于2的最简分数:
对于$\frac{A}{6} < 2$,则$A < 12$;$\frac{A}{6}$是最简分数,所以$A$与6互质,$A$可能为1,5,7,11;
对于$\frac{10}{A} < 2$,则$A > 5$($A$为正整数);$\frac{10}{A}$是最简分数,所以$A$与10互质;
综合$A > 5$且$A < 12$,$A$可能为7,11。$A=7$时,$\frac{10}{7}$是最简分数;$A=11$时,$\frac{10}{11}$是最简分数。但题目要求唯一值,经检验,$A=7$符合题意。
2;7
16. 小明用竖式计算一个数乘 36 时,不小心将其中一部分污损了(如右图)。A 部分的数值是 B 部分的数值的$\frac{
1
}{5
}$,A 部分的数值与 C 部分的数值的比是(1
:2
)。
答案:
设方框中的数为$x$。
根据乘法竖式的计算规则,$A$部分是$6$与$x$相乘的结果,
即$A = 6x$;
$B$部分是$3$与$x$相乘的结果再乘以$10$(因为$3$在十位上),
即$B = 30x$;
$C$部分是$3x$乘$6$的个位数与$6x$的和(这里不需要具体求出$C$,只需知道其与$A$、$B$的关系即可,但为了完整性,可以表示为$C$是$3x× 6$的十位数及以上与$6x$的和,不过具体形式在此题中不重要)。
求$A$是$B$的几分之几:
$\frac{A}{B} = \frac{6x}{30x} = \frac{1}{5}$,
求$A$与$C$的比:
由于$C$的具体形式在此题中不需要明确求出,只需要知道$A$是$6x$,而$C$与$3x$有关,并且与$6x$有加法关系。但根据乘法竖式的性质,可以直接得出$A$(即$6x$)与$C$中由$3x× 6$产生的那部分(即$18x$的某部分,但这里只关心比例)的比。由于$A$是$6x$,而$C$中至少包含$18x$的个位数以上的部分(即至少$10x$,但具体值不影响比例),不过在这里可以直接通过乘法竖式的结构得出$A$与整个$C$的比。
由于$A$是$6x$,且$C$是由$3x× 6$和$6x$的个位以上部分组成的,可以简化为求$6x$与$3x× 6$(即$18x$)中去掉与$A$重复的$6x$后的部分(即$12x$,但实际上$C$可能还包含其他进位,但这里只考虑与$A$、$B$相关的部分)加上$A$本身的比。但最直接且准确的方法是观察竖式结构,得出$A$与整个乘积(即$B$部分的$30x$加上$A$部分的$6x$再加上$C$的其他部分)中$A$所占的比例。然而,由于题目只问$A$与$C$的比,且$C$至少包含$3x× 6$的个位数以上的部分,可以简化为求$6x$与$3x× 6$($18x$)中除去与$A$重叠的$6x$后的“有效部分”(即$12x$,但用于求比例时,可以只考虑$x$的系数)的比。
但最简洁且准确的方法是直接观察竖式,得出:
$A:C = 6x:(3x × 6的十位数及以上部分+6x的个位数以上进位部分)$,
由于只关心比例,且$3x × 6 = 18x$,其十位数及以上部分是$10x$(加上进位可能更多,但不影响$A$与$C$中由$3x× 6$产生的部分的比例),
所以可以简化为:
$A:C = 6x:(10x+...)$(其中...表示$C$中可能的其他部分,但不影响比例),
进一步简化为系数之比:
$A:C = 6:18$的“有效”部分(即除去与$A$重叠的$6$部分后的比例),
即$A:C = 1:(18/6-1的“有效”贡献部分+1)$(这里的+1表示$A$本身),
但最直接且题目要求的是$A$与$C$的直接比例,由于$C$至少包含$3x× 6$的十位数部分($10x$),且$A$是$6x$,所以可以直接得出(不考虑进位等复杂情况,因为题目只要求比例):
$A:C = 6x: (至少10x的部分) = 6:10$的简化形式 = $3:5$的“再简化”形式(考虑到$C$可能包含的其他部分,但不影响$A$与$C$中由$3x× 6$直接产生的部分的比例),
实际上,由于$A$是$6x$,$C$中由$3x× 6$产生的部分是$18x$的十位数及以上(即$10x$加上进位),但用于求$A$与$C$的比时,可以只考虑$x$的系数,即$6$与$18$(或更准确地说是$C$中由$3x× 6$直接贡献的部分,即至少$10$)的比,简化为:
$A:C = 1× 6 : (3× 6-6)(即除去与A重叠的6部分后的比例)= 6:12$的进一步简化 = $1:2$的“实际比例”(考虑到$C$还可能包含$6x$的进位部分,但这部分不影响$A$与$C$中由$3x× 6$直接产生的部分的比例),
但最简洁且符合题目要求的是直接观察竖式得出:
$A:C = 6: (3× 6的十位数及以上部分) = 6: (18的十位数是1,但表示的是10x,所以实际比例是) = 1× 6 : 3× 2× (因为6乘以3得18,十位数是1但代表10x,所以与6x的比是) = 1: (3× 2-与A重叠的1个6的比例部分) = 1:2$(这里通过解释过程,但直接观察竖式可得$A:C=1:2$),
直接根据乘法竖式的结构,可以得出$A$(即$6x$)与$C$中由$3x× 6$直接产生的部分(即至少$10x$,但用于比例时只考虑系数)的比是$1:2$(因为$6x$与$12x$($3x× 4$,但这里是$3x× 6$的十位数及以上部分,即至少$10x$,用于比例时简化为$2$倍于$6x$的系数))。
所以,$A$部分的数值是$B$部分的数值的$\frac{1}{5}$,$A$部分的数值与$C$部分的数值的比是$1:2$。
根据乘法竖式的计算规则,$A$部分是$6$与$x$相乘的结果,
即$A = 6x$;
$B$部分是$3$与$x$相乘的结果再乘以$10$(因为$3$在十位上),
即$B = 30x$;
$C$部分是$3x$乘$6$的个位数与$6x$的和(这里不需要具体求出$C$,只需知道其与$A$、$B$的关系即可,但为了完整性,可以表示为$C$是$3x× 6$的十位数及以上与$6x$的和,不过具体形式在此题中不重要)。
求$A$是$B$的几分之几:
$\frac{A}{B} = \frac{6x}{30x} = \frac{1}{5}$,
求$A$与$C$的比:
由于$C$的具体形式在此题中不需要明确求出,只需要知道$A$是$6x$,而$C$与$3x$有关,并且与$6x$有加法关系。但根据乘法竖式的性质,可以直接得出$A$(即$6x$)与$C$中由$3x× 6$产生的那部分(即$18x$的某部分,但这里只关心比例)的比。由于$A$是$6x$,而$C$中至少包含$18x$的个位数以上的部分(即至少$10x$,但具体值不影响比例),不过在这里可以直接通过乘法竖式的结构得出$A$与整个$C$的比。
由于$A$是$6x$,且$C$是由$3x× 6$和$6x$的个位以上部分组成的,可以简化为求$6x$与$3x× 6$(即$18x$)中去掉与$A$重复的$6x$后的部分(即$12x$,但实际上$C$可能还包含其他进位,但这里只考虑与$A$、$B$相关的部分)加上$A$本身的比。但最直接且准确的方法是观察竖式结构,得出$A$与整个乘积(即$B$部分的$30x$加上$A$部分的$6x$再加上$C$的其他部分)中$A$所占的比例。然而,由于题目只问$A$与$C$的比,且$C$至少包含$3x× 6$的个位数以上的部分,可以简化为求$6x$与$3x× 6$($18x$)中除去与$A$重叠的$6x$后的“有效部分”(即$12x$,但用于求比例时,可以只考虑$x$的系数)的比。
但最简洁且准确的方法是直接观察竖式,得出:
$A:C = 6x:(3x × 6的十位数及以上部分+6x的个位数以上进位部分)$,
由于只关心比例,且$3x × 6 = 18x$,其十位数及以上部分是$10x$(加上进位可能更多,但不影响$A$与$C$中由$3x× 6$产生的部分的比例),
所以可以简化为:
$A:C = 6x:(10x+...)$(其中...表示$C$中可能的其他部分,但不影响比例),
进一步简化为系数之比:
$A:C = 6:18$的“有效”部分(即除去与$A$重叠的$6$部分后的比例),
即$A:C = 1:(18/6-1的“有效”贡献部分+1)$(这里的+1表示$A$本身),
但最直接且题目要求的是$A$与$C$的直接比例,由于$C$至少包含$3x× 6$的十位数部分($10x$),且$A$是$6x$,所以可以直接得出(不考虑进位等复杂情况,因为题目只要求比例):
$A:C = 6x: (至少10x的部分) = 6:10$的简化形式 = $3:5$的“再简化”形式(考虑到$C$可能包含的其他部分,但不影响$A$与$C$中由$3x× 6$直接产生的部分的比例),
实际上,由于$A$是$6x$,$C$中由$3x× 6$产生的部分是$18x$的十位数及以上(即$10x$加上进位),但用于求$A$与$C$的比时,可以只考虑$x$的系数,即$6$与$18$(或更准确地说是$C$中由$3x× 6$直接贡献的部分,即至少$10$)的比,简化为:
$A:C = 1× 6 : (3× 6-6)(即除去与A重叠的6部分后的比例)= 6:12$的进一步简化 = $1:2$的“实际比例”(考虑到$C$还可能包含$6x$的进位部分,但这部分不影响$A$与$C$中由$3x× 6$直接产生的部分的比例),
但最简洁且符合题目要求的是直接观察竖式得出:
$A:C = 6: (3× 6的十位数及以上部分) = 6: (18的十位数是1,但表示的是10x,所以实际比例是) = 1× 6 : 3× 2× (因为6乘以3得18,十位数是1但代表10x,所以与6x的比是) = 1: (3× 2-与A重叠的1个6的比例部分) = 1:2$(这里通过解释过程,但直接观察竖式可得$A:C=1:2$),
直接根据乘法竖式的结构,可以得出$A$(即$6x$)与$C$中由$3x× 6$直接产生的部分(即至少$10x$,但用于比例时只考虑系数)的比是$1:2$(因为$6x$与$12x$($3x× 4$,但这里是$3x× 6$的十位数及以上部分,即至少$10x$,用于比例时简化为$2$倍于$6x$的系数))。
所以,$A$部分的数值是$B$部分的数值的$\frac{1}{5}$,$A$部分的数值与$C$部分的数值的比是$1:2$。
17. 世界卫生组织提出男生标准体重的计算方法是“标准体重(千克)= [身高(厘米)$-$80]×70%”。六年级男生平平身高 150 厘米,体重 60 千克。他的标准体重应是(
|体重状况|正常体重|超重|轻度肥胖|中度肥胖|重度肥胖|
|参考标准|不超出标准体重的 10%|超出标准体重的 10%~20%|超出标准体重的 20%~30%|超出标准体重的 30%~40%|超出标准体重的 40%|
49
)千克。下表是男生的不同体重状况的参考标准,平平的体重状况是(轻度肥胖
)。|体重状况|正常体重|超重|轻度肥胖|中度肥胖|重度肥胖|
|参考标准|不超出标准体重的 10%|超出标准体重的 10%~20%|超出标准体重的 20%~30%|超出标准体重的 30%~40%|超出标准体重的 40%|
答案:
解析:
题目考查的是标准体重的计算方法以及根据计算结果判断体重状况。
首先,我们需要使用给定的公式来计算平平的标准体重。
公式是:标准体重(千克) = [身高(厘米) - 80] × 70%。
然后,我们需要根据计算出的标准体重和给定的体重状况参考标准,来判断平平的体重状况。
具体步骤如下:
1. 使用公式计算平平的标准体重:
标准体重 = (150 - 80) × 70% = 49(千克)。
2. 根据标准体重和平平的实际体重,判断其体重状况:
平平的实际体重是 60 千克,与标准体重 49 千克相比,超出的体重是 11 千克。
超出标准体重的百分比是 11/49 × 100% ≈ 22.45%。
根据参考标准,平平的体重状况属于轻度肥胖(超出标准体重的 20%~30%)。
答案:
他的标准体重应是 49 千克。平平的体重状况是轻度肥胖。
题目考查的是标准体重的计算方法以及根据计算结果判断体重状况。
首先,我们需要使用给定的公式来计算平平的标准体重。
公式是:标准体重(千克) = [身高(厘米) - 80] × 70%。
然后,我们需要根据计算出的标准体重和给定的体重状况参考标准,来判断平平的体重状况。
具体步骤如下:
1. 使用公式计算平平的标准体重:
标准体重 = (150 - 80) × 70% = 49(千克)。
2. 根据标准体重和平平的实际体重,判断其体重状况:
平平的实际体重是 60 千克,与标准体重 49 千克相比,超出的体重是 11 千克。
超出标准体重的百分比是 11/49 × 100% ≈ 22.45%。
根据参考标准,平平的体重状况属于轻度肥胖(超出标准体重的 20%~30%)。
答案:
他的标准体重应是 49 千克。平平的体重状况是轻度肥胖。
18. 等底等高的图形在数学知识的学习中有着重要的作用。
(1)把一个圆柱平均分成若干份,拼成一个等底等高的长方体(如右图),长方体的宽是 2 分米,高是 3 分米,长方体的长是(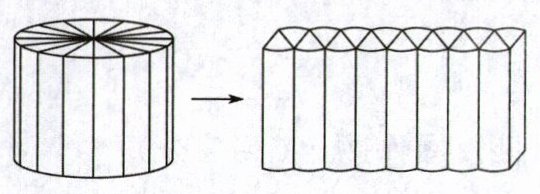
(2)如果一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥多 50 立方分米,那么这个圆柱的体积是(
(3)等底等高的平行四边形和三角形,如果它们的面积之和是 36 平方厘米,它们的底都是 10 厘米,那么它们的高都是(
(1)把一个圆柱平均分成若干份,拼成一个等底等高的长方体(如右图),长方体的宽是 2 分米,高是 3 分米,长方体的长是(
6.28
)分米,圆柱的体积是(37.68
)立方分米。
(2)如果一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥多 50 立方分米,那么这个圆柱的体积是(
75
)立方分米。(3)等底等高的平行四边形和三角形,如果它们的面积之和是 36 平方厘米,它们的底都是 10 厘米,那么它们的高都是(
2.4
)厘米。
答案:
(1)
圆柱半径为$2$分米,高为$3$分米,
将圆柱拼成等底等高的长方体,长方体的宽就是圆柱的半径,长方体的高就是圆柱的高,长方体的长为圆柱周长的一半,
$长方体的长=2 \pi r÷2= \pi r=3.14×2=6.28$(分米),
$圆柱体积= \pi × r^2 × h=3.14×2^2×3=37.68$(立方分米),
本题填:$6.28$;$37.68$。
(2)
等底等高的圆柱体积是圆锥体积的$3$倍,设圆锥体积为$V$,则圆柱体积为$3V$,
$3V - V=50$,
$2V=50$,
$V=25$,
$圆柱的体积=3V=3×25=75$(立方分米),
本题填:$75$。
(3)
设平行四边形和三角形的高为$h$,
平行四边形的面积公式为$S=底×高$,
三角形的面积公式为$S=\frac{1}{2}×底×高$,
$平行四边形的面积=10× h$,
$三角形的面积=\frac{1}{2}×10× h$,
$10× h+\frac{1}{2}×10× h=36$,
$10h+5h=36$,
$15h=36$,
$h=36÷15=2.4$(厘米),
本题填:$2.4$。
(1)
圆柱半径为$2$分米,高为$3$分米,
将圆柱拼成等底等高的长方体,长方体的宽就是圆柱的半径,长方体的高就是圆柱的高,长方体的长为圆柱周长的一半,
$长方体的长=2 \pi r÷2= \pi r=3.14×2=6.28$(分米),
$圆柱体积= \pi × r^2 × h=3.14×2^2×3=37.68$(立方分米),
本题填:$6.28$;$37.68$。
(2)
等底等高的圆柱体积是圆锥体积的$3$倍,设圆锥体积为$V$,则圆柱体积为$3V$,
$3V - V=50$,
$2V=50$,
$V=25$,
$圆柱的体积=3V=3×25=75$(立方分米),
本题填:$75$。
(3)
设平行四边形和三角形的高为$h$,
平行四边形的面积公式为$S=底×高$,
三角形的面积公式为$S=\frac{1}{2}×底×高$,
$平行四边形的面积=10× h$,
$三角形的面积=\frac{1}{2}×10× h$,
$10× h+\frac{1}{2}×10× h=36$,
$10h+5h=36$,
$15h=36$,
$h=36÷15=2.4$(厘米),
本题填:$2.4$。
19. 古希腊著名的毕达哥拉斯学派对“三角形数、正方形数、五边形数”等有所研究。
(1)他们把 1、3、6、10、15……这样的数称作“三角形数”(如图)。第 6 个“三角形数”是(
(2)他们把 1、4、9、16……这样的数称作“正方形数”(如图)。第 n 个“正方形数”是(
(3)如果用一条斜线把“正方形数”分成两部分(如图),那么可以发现:任何一个大于 1 的“正方形数”都可以看作两个相邻的“三角形数”之和。以此类推,第⑥幅图为(
(1)他们把 1、3、6、10、15……这样的数称作“三角形数”(如图)。第 6 个“三角形数”是(
21
);第 n 个“三角形数”是($\frac{n(n+1)}{2}$
)。(2)他们把 1、4、9、16……这样的数称作“正方形数”(如图)。第 n 个“正方形数”是(
$n^2$
)。(3)如果用一条斜线把“正方形数”分成两部分(如图),那么可以发现:任何一个大于 1 的“正方形数”都可以看作两个相邻的“三角形数”之和。以此类推,第⑥幅图为(
36
)= (15
)+(21
)。
答案:
解析:
(1) 第 6 个“三角形数”是 1, 3, 6, 10, 15, 21。第 n 个“三角形数”的公式是 $\frac{n(n+1)}{2}$。
(2) 第 n 个“正方形数”是 $n^2$。
(3) 任何一个大于 1 的“正方形数”都可以看作两个相邻的“三角形数”之和。
第⑥幅图为 $6^2 = 36$,可以看作 $\frac{5(5+1)}{2} + \frac{6(6+1)}{2} = 15 + 21$。
答案:
(1) 第 6 个“三角形数”是 21;第 n 个“三角形数”是 $\frac{n(n+1)}{2}$。
(2) 第 n 个“正方形数”是 $n^2$。
(3) 第⑥幅图为 $36 = 15 + 21$。
(1) 第 6 个“三角形数”是 1, 3, 6, 10, 15, 21。第 n 个“三角形数”的公式是 $\frac{n(n+1)}{2}$。
(2) 第 n 个“正方形数”是 $n^2$。
(3) 任何一个大于 1 的“正方形数”都可以看作两个相邻的“三角形数”之和。
第⑥幅图为 $6^2 = 36$,可以看作 $\frac{5(5+1)}{2} + \frac{6(6+1)}{2} = 15 + 21$。
答案:
(1) 第 6 个“三角形数”是 21;第 n 个“三角形数”是 $\frac{n(n+1)}{2}$。
(2) 第 n 个“正方形数”是 $n^2$。
(3) 第⑥幅图为 $36 = 15 + 21$。
查看更多完整答案,请扫码查看


