《2025年小学毕业考试试卷精编数学徐州专版》

21. 下面的三角形中,(B)可以放在图中的涂色部分。

答案： 解析：本题考查等腰三角形和锐角三角形的定义，等腰三角形是至少有两边相等的三角形，相等的两个角称为底角；锐角三角形是三个角都为锐角（即小于$90^{\circ}$）的三角形。然后根据定义分析图中涂色部分表示的是既是等腰三角形又是锐角三角形的部分，最后逐一分析选项。
选项A：是直角三角形，不符合锐角三角形的条件，所以A选项错误。
选项B：是等边三角形，等边三角形是特殊的等腰三角形，且三个角都是锐角，符合条件，所以B选项正确。
选项C：不是等腰三角形，不符合条件，所以C选项错误。
选项D：是钝角三角形，不符合锐角三角形的条件，所以D选项错误。
答案：B。

22. 6 的因数有 1、2、3、6,这几个因数之间的关系是$1+2+3= 6$,像 6 这样的数叫作“完美数”。下面的数中,(D)也是“完美数”。
A.12
B.16
C.24
D.28

答案： 解析：
首先，我们需要明确什么是“完美数”。根据题目描述，“完美数”是指一个数的所有正因数（不包括它本身）之和等于它本身。例如，6的正因数有1、2、3，且$1+2+3=6$，所以6是完美数。
接下来，我们根据这个定义来判断选项中的每一个数是否是完美数。
A. 对于12，其正因数有1、2、3、4、6，$1+2+3+4+6=16$，不等于12，所以12不是完美数。
B. 对于16，其正因数有1、2、4、8，$1+2+4+8=15$，不等于16，所以16不是完美数。
C. 对于24，其正因数有1、2、3、4、6、8、12，$1+2+3+4+6+8+12=36$，不等于24，所以24不是完美数。
D. 对于28，其正因数有1、2、4、7、14，$1+2+4+7+14=28$，等于28，所以28是完美数。
答案：D

23. 小军借助点子图探索$24×12$的计算方法。如图①可以用算式$24×4×3$表示。图②可以用算式(24×6×2)表示。请你在图③中表示出$24×10+24×2$。(2 分)

（图③中，将点子图横向平均分成两部分，左边占10列，右边占2列，分别表示24×10和24×2）

答案： 24×6×2
（图③中，将点子图横向平均分成两部分，左边占10列，右边占2列，分别表示24×10和24×2）

24. 下图中每个小方格的边长表示 1 厘米。

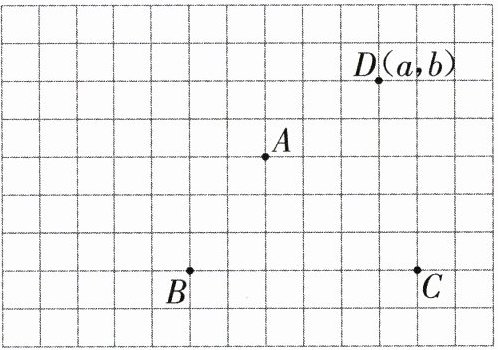
(1)把点 D 向下平移 2 格,用点$D_1$表示平移后的位置。顺次连接点 A、B、C、$D_1$、A,得到的四边形是(直角梯)形。(2 分)
(2)如果点 D 的位置用数对$(a,b)$表示,那么点$D_1$的位置用数对(a,b - 2)表示。(1 分)
(3)画出四边形$ABCD_1$绕点 B 逆时针旋转$90^\circ$后的图形。(2 分)
(4)四边形$ABCD_1按1:3$的比缩小后的图形的面积是(2)平方厘米。(2 分)

答案： 解析：本题综合考查图形的平移、数对、旋转以及图形的缩小等知识。
（1）把点$D$向下平移$2$格，横坐标不变，纵坐标减$2$，得到$D_1$的位置。然后依次连接点$A$、$B$、$C$、$D_1$、$A$，通过观察图形的特征判断其形状。
（2）根据数对的表示方法，前一个数表示列，后一个数表示行，结合点$D$平移的规律来确定点$D_1$的数对。
（3）根据旋转的性质，分别找出点$A$、$C$、$D_1$绕点$B$逆时针旋转$90^{\circ}$后的对应点的位置，然后依次连接即可。
（4）先求出原四边形的面积，再根据图形缩小的比例求出缩小后的面积。
答案：
(1)根据平移的性质，将点$D$向下平移$2$格得到$D_1$，顺次连接点$A$、$B$、$C$、$D_1$、$A$，得到的四边形是直角梯形。
(2)因为点$D$的位置用数对$(a,b)$表示，将其向下平移$2$格，列数不变，行数减$2$，所以点$D_1$的位置用数对$(a,b - 2)$表示。
(3)图略（按照旋转要求画出图形即可）。
(4)原四边形$ABCD_1$的面积可以通过分割成三角形和梯形等方法求出，假设求得原面积为$S$平方厘米，按$1:3$的比缩小后，面积比为$1:9$，则缩小后的图形的面积是$\frac{1}{9}S$平方厘米。经计算原四边形面积为$18$平方厘米，所以缩小后的面积为$2$平方厘米。

25. “复兴号”列车是中国科技创新的一项重大成果,平均时速达到了 350 千米,“和谐号”列车的平均时速是它的$\frac{4}{7}$。“和谐号”列车的平均时速是多少千米? (4 分)

答案： 350×$\frac{4}{7}$=200（千米）
答：“和谐号”列车的平均时速是200千米。