《2025年小学毕业考试试卷精编数学徐州专版》

16. 据记载,三国名将关羽“身长九尺”,特别高大威武,其中的“尺”是古代长度单位。在现代,1 尺≈33.33 厘米。有趣的是,在不同的历史时期,“1 尺”的标准是不同的(如图)。联系实际想一想,朝代(②)的标准最有可能是三国时期“1 尺”的标准。
朝代①:1 尺≈16.95 厘米 朝代②:1 尺≈24.2 厘米
朝代③:1 尺≈29.6 厘米 朝代④:1 尺≈31.68 厘米

答案： 解析：题目考查不同历史时期长度单位“尺”的标准，以及生活常识。
在现代1尺≈33.33厘米，三国名将关羽“身长九尺”，若按现代标准关羽身高约为$33.33×9 = 299.97$厘米，这显然过高不符合实际。
所以三国时期“1尺”的标准应小于现代1尺的标准。
分析各个选项：
朝代①：1尺≈16.95厘米，若按此标准，关羽身高约为$16.95×9 = 152.55$厘米，对于名将来说可能偏矮。
朝代②：1尺≈24.2厘米，关羽身高约为$24.2×9 = 217.8$厘米，比较符合名将高大威武的形象。
朝代③：1尺≈29.6厘米，关羽身高约为$29.6×9 = 266.4$厘米，相对较高。
朝代④：1尺≈31.68厘米，关羽身高约为$31.68×9 = 285.12$厘米，更接近现代标准，过高。
综合比较，朝代②的标准最有可能是三国时期“1尺”的标准。
答案：朝代②

17. 把一个底面直径和高都是 4 cm 的圆柱的侧面沿虚线剪开,得到一个不规则图形(如左下图),这个不规则图形的面积是(50.24)$cm^2$;如果给原来的这个圆柱做一个正方体包装盒,那么至少需要硬纸板(96)$cm^2$(接头处忽略不计)。

答案： 圆柱的侧面积公式为$S = \pi d h$，其中$d$为底面直径，$h$为圆柱的高。
已知圆柱底面直径$d = 4cm$，高$h = 4cm$，$\pi$取$3.14$，则侧面积为：
$S = 3.14× 4× 4 = 50.24$（$cm^2$）。
所以这个不规则图形的面积是$50.24cm^2$。
要给原来的圆柱做一个正方体包装盒，正方体的棱长至少要等于圆柱的底面直径和高中的较大值。
因为圆柱底面直径和高都是$4cm$，所以正方体的棱长$a = 4cm$。
正方体的表面积公式为$S = 6a^2$，则正方体包装盒的表面积为：
$S = 6× 4^2 = 6× 16 = 96$（$cm^2$）。
答案：$50.24$；$96$。

18. 如右上图,把三角形 ABC 的边 AC 延长到点 D,那么∠1+∠2(=)∠4(填“＞”“＜”或“=”)。

答案： 解析：三角形内角和为$180^\circ$，在$\bigtriangleup ABC$中，$\angle 1 + \angle 2 + \angle 3=180^{\circ}$ ，而$\angle 3$与$\angle 4$组成平角，即$\angle 3+\angle 4 = 180^{\circ}$，所以$\angle 3=180^{\circ}-\angle 4$。
把$\angle 3=180^{\circ}-\angle 4$代入$\angle 1 + \angle 2 + \angle 3=180^{\circ}$可得：
$\angle 1 + \angle 2+180^{\circ}-\angle 4 = 180^{\circ}$，
移项后得到$\angle 1 + \angle 2=\angle 4$。
答案：=

19. 在数学上,图形可以通过一种特殊的方式“生长”。以一个正三角形(如图①)为例,将它的三条边分别三等分,然后以每条边中间的一段为底边,向外再画出一个等边三角形,并擦去原来中间的那一段,这时,图形就完成了一次“生长”变形,成为一个新图形(如图②)。

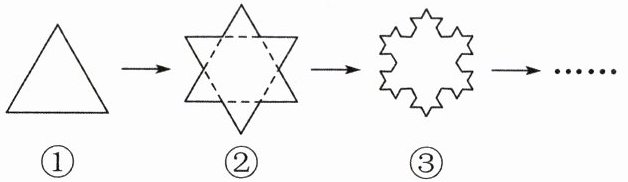
(1) 如果一个边长是 27 厘米的等边三角形像这样经过两次“生长”变形,那么得到的图形(如图③)的周长是(144)厘米。
(2) 如果一个边长为 a 厘米的等边三角形像这样经过四次“生长”变形,那么得到的图形的周长是($\frac{256a}{27}$)厘米(用含有 a 的式子表示)。

答案： 1. （1）
首先分析一次“生长”后周长的变化：
设原正三角形边长为$b$。原正三角形周长$C_0 = 3b$。
一次“生长”时，每条边变为原来的$\frac{4}{3}$（因为把一条边三等分，去掉一段，增加两段，相当于每条边的长度变为原来的$1+\frac{1}{3}=\frac{4}{3}$）。
当$b = 27$厘米时，原三角形周长$C_0=3×27 = 81$厘米。
一次“生长”后周长$C_1=\frac{4}{3}C_0$，二次“生长”后周长$C_2=\frac{4}{3}C_1$。
所以$C_2=\left(\frac{4}{3}\right)^2C_0$。
把$C_0 = 81$代入可得：$C_2=\left(\frac{4}{3}\right)^2×81=\frac{16}{9}×81 = 144$厘米。
2. （2）
由（1）的规律可得：
原三角形周长$C_0 = 3a$。
一次“生长”后周长$C_1=\frac{4}{3}C_0$，二次“生长”后周长$C_2=\frac{4}{3}C_1=\left(\frac{4}{3}\right)^2C_0$，三次“生长”后周长$C_3=\frac{4}{3}C_2=\left(\frac{4}{3}\right)^3C_0$，四次“生长”后周长$C_4=\frac{4}{3}C_3=\left(\frac{4}{3}\right)^4C_0$。
因为$C_0 = 3a$，所以$C_4=\left(\frac{4}{3}\right)^4×3a$。
计算$\left(\frac{4}{3}\right)^4×3a=\frac{256}{81}×3a=\frac{256a}{27}$。
故答案依次为：（1）$144$；（2）$\frac{256a}{27}$。

20. 古埃及人总喜欢把分数转化成分子是 1 的分数来计算,所以后人常把分子是 1 的分数称为埃及分数。埃及分数在计算中有着重要的规律:$\frac{1}{n×(n+1)}= \frac{1}{n}-\frac{1}{n+1}$(n 是非 0 自然数)。例如,$\frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$。请根据这个规律,计算$\frac{2}{3×4}+\frac{2}{4×5}+\frac{2}{5×6}+\frac{2}{6×7}+…+\frac{2}{2022×2023}+\frac{2}{2023×2024}= $($\frac{2021}{3036}$)。

答案： $\begin{aligned}&\frac{2}{3×4}+\frac{2}{4×5}+\frac{2}{5×6}+\cdots+\frac{2}{2023×2024}\\=&2×\left(\frac{1}{3×4}+\frac{1}{4×5}+\frac{1}{5×6}+\cdots+\frac{1}{2023×2024}\right)\\=&2×\left[\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{6}\right)+\cdots+\left(\frac{1}{2023}-\frac{1}{2024}\right)\right]\\=&2×\left(\frac{1}{3}-\frac{1}{2024}\right)\\=&2×\left(\frac{2024}{3×2024}-\frac{3}{3×2024}\right)\\=&2×\frac{2021}{6072}\\=&\frac{2021}{3036}\end{aligned}$
$\boxed{\frac{2021}{3036}}$

21. 如图,正六边形的边长是 3 厘米,圆的半径是 1 厘米。当圆绕着正六边形滚动一周又回到原来位置时,圆心 O 经过的路程是(24.28)厘米,圆扫过的面积是(48.56)平方厘米。

答案： 圆心经过的路程：正六边形周长为 $6×3 = 18$ 厘米，圆滚动时圆心绕正六边形外角滚动的轨迹为一个圆，半径为1厘米，正六边形外角和为 $360^\circ$，即一个整圆，其周长为 $2×3.14×1 = 6.28$ 厘米，总路程为 $18 + 6.28 = 24.28$ 厘米。
圆扫过的面积：包括6个长方形和一个半径为2厘米的圆的面积。长方形面积为 $3×2×6 = 36$ 平方厘米，圆的面积为 $3.14×2^2 = 12.56$ 平方厘米，总面积为 $36 + 12.56 = 48.56$ 平方厘米。
24.28，48.56

22. 直接写出得数。(8 分)
2.4×0.5=1.2 $\frac{5}{6}÷\frac{1}{8}=$$\frac{20}{3}$ 10.05-9.5=0.55 4÷$\frac{2}{3}=$6
$(\frac{2}{3}-\frac{1}{4})×24=$10 1÷$\frac{2}{3}×\frac{3}{2}=$$\frac{9}{4}$ 0.25^3=0.015625 $\frac{2}{3}+\frac{1}{3}×2=$$\frac{4}{3}$

答案： 解析：
题目考查的知识点主要是基本的四则运算、分数运算以及简单的代数表达式求值。
答案：
$2.4×0.5=1.2$
$\frac{5}{6}÷\frac{1}{8}=\frac{5}{6} × 8 = \frac{40}{6} = \frac{20}{3}$
$10.05-9.5=0.55$
$4÷\frac{2}{3}=4 × \frac{3}{2} = 6$
$(\frac{2}{3}-\frac{1}{4})×24 = (\frac{8}{12}-\frac{3}{12})×24 = \frac{5}{12} × 24 = 10$
$1÷\frac{2}{3}×\frac{3}{2}=1 × \frac{3}{2} × \frac{3}{2} = \frac{9}{4}$
$0.25^3=0.25 × 0.25 × 0.25 = 0.015625$
$\frac{2}{3}+\frac{1}{3}×2=\frac{2}{3}+\frac{2}{3}=\frac{4}{3}$