《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1 (浙江宁波鄞州区自主招生)如图，AB是⊙O的直径，点C是⊙O上一点，连接AC，过点C作直线CD⊥AB于点D，点E是DB上任意一点(点D，B除外)，直线CE交⊙O于点F，连接AF与直线CD交于点G.若AG=2，GF=4，则AC=________.
　　　　　　　　　　　　　

答案：
$2\sqrt{3}$ [解析]如图，连接 $CB$.
∵ $AB$ 是 $\odot O$ 的直径，$CD\perp AB$，
∴ $\angle ACB=\angle ADC=\angle BDC = 90^{\circ}$，
∴ $\angle ACD+\angle BCD=\angle ABC+\angle BCD = 90^{\circ}$，
∴ $\angle ACG=\angle ABC=\angle AFC$.
又 $\angle CAG=\angle FAC$，
∴ $\triangle ACG\sim\triangle AFC$，
∴ $\frac{AC}{AF}=\frac{AG}{AC}$，
∴ $AC^{2}=AG\cdot AF = AG\cdot(AG + GF)=2\times(2 + 4)=12$，
∴ $AC = 2\sqrt{3}$（负值舍去）.

2 如图，在⊙O中，直径CD⊥弦AB于点E，AM⊥BC于点M，交CD于点N，连接AD.
(1)求证：AD=AN；
(2)若AB=2$\sqrt{15}$，ON=2OE，求⊙O的半径.
　　　　　　　　　　　　　

答案：
(1)
∵ $CD\perp AB$，
∴ $\angle CEB = 90^{\circ}$，
∴ $\angle C+\angle B = 90^{\circ}$.
同理 $\angle C+\angle CNM = 90^{\circ}$，
∴ $\angle CNM=\angle B$.
∵ $\angle CNM=\angle AND$，
∴ $\angle AND=\angle B$.
∵ $\angle D=\angle B$，
∴ $\angle AND=\angle D$，
∴ $AD = AN$.
(2)连接 $OA$，设 $OE$ 的长为 $x$，则 $ON = 2x$.
∵ $AN = AD$，$CD\perp AB$，
∴ $DE = NE = 3x$，
∴ $OD = OE + ED=x + 3x = 4x$，
∴ $OA = OD = 4x$.
∵ $AB\perp CD$，$AB = 2\sqrt{15}$，
∴ $AE=\sqrt{15}$.
在 $Rt\triangle OAE$ 中，$OE^{2}+AE^{2}=OA^{2}$，
∴ $x^{2}+(\sqrt{15})^{2}=(4x)^{2}$，解得 $x = 1$（负值舍去），
∴ $OA = 4$，即 $\odot O$ 的半径为 $4$.

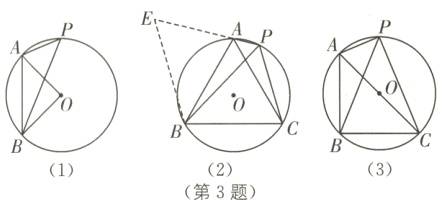
3 中考新考法 操作探究 (2023·长春中考)[感知]如图(1)，点A，B，P均在⊙O上，∠AOB=90°，则锐角∠APB的大小为________度.
[探究]小明遇到这样一个问题：如图(2)，⊙O是等边三角形ABC的外接圆，点P在$\overset{\frown}{AC}$上(点P不与点A，C重合)，连接PA，PB，PC.求
证：PB=PA+PC. 小明发现，延长PA至点E，使AE=PC，连接BE，通过证明△PBC≌△EBA，可推得△PBE是等边三角形，进而得证. 下面是小明的部分证明过程：
证明：延长PA至点E，使AE=PC，连接BE.
∵四边形ABCP是⊙O的内接四边形，
∴∠BAP+∠BCP=180°.
∵∠BAP+∠BAE=180°，∴∠BCP=∠BAE.
∵△ABC是等边三角形，∴BA=BC，
∴△PBC≌△EBA(SAS).
请你补全余下的证明过程.
[应用]如图(3)，⊙O是△ABC的外接圆，∠ABC=90°，AB=BC，点P在⊙O上，且点P与点B在AC的两侧，连接PA，PB，PC，若PB=2$\sqrt{2}$PA，则$\frac{PB}{PC}$的值为________.
　　　　　　　　

答案：
[感知] $45$ [解析]
∵ $\angle AOB = 90^{\circ}$，
∴ $\angle APB=\frac{1}{2}\angle AOB = 45^{\circ}$（在同圆中，同弧所对的圆周角是圆心角的一半）.
[探究]延长 $PA$ 至点 $E$，使 $AE = PC$，连接 $BE$.
∵ 四边形 $ABCP$ 是 $\odot O$ 的内接四边形，
∴ $\angle BAP+\angle BCP = 180^{\circ}$.
∵ $\angle BAP+\angle BAE = 180^{\circ}$，
∴ $\angle BCP=\angle BAE$.
∵ $\triangle ABC$ 是等边三角形，
∴ $BA = BC$，
∴ $\triangle PBC\cong\triangle EBA(SAS)$，
∴ $PB = EB$.
又 $\triangle ABC$ 是等边三角形，
∴ $\angle ACB = 60^{\circ}$，
∴ $\angle APB = 60^{\circ}$，
∴ $\triangle PBE$ 为等边三角形，
∴ $PB = PE = AP + AE = PA + PC$.
[应用] $\frac{2\sqrt{2}}{3}$ [解析]如图，延长 $PA$ 至点 $G$，使 $AG = PC$，连接 $BG$.
∵ 四边形 $ABCP$ 是 $\odot O$ 的内接四边形，
∴ $\angle BAP+\angle BCP = 180^{\circ}$.
∵ $\angle BAP+\angle BAG = 180^{\circ}$，
∴ $\angle BCP=\angle BAG$.

在 $\triangle PBC$ 和 $\triangle GBA$ 中，$\begin{cases}PC = GA\\\angle BCP=\angle BAG\\BC = BA\end{cases}$，
∴ $\triangle PBC\cong\triangle GBA(SAS)$，
∴ $PB = GB$，$\angle PBC=\angle GBA$.
∵ $\angle ABC = 90^{\circ}$，
∴ $\angle PBG=\angle GBA+\angle ABP=\angle PBC+\angle ABP=\angle ABC = 90^{\circ}$，
∴ $PG=\sqrt{2}BP$.
∵ $PG = PA + AG = PA + PC$，$PB = 2\sqrt{2}PA$，
∴ $PC = PG - PA=\sqrt{2}\times2\sqrt{2}PA - PA = 3PA$，
∴ $\frac{PB}{PC}=\frac{2\sqrt{2}PA}{3PA}=\frac{2\sqrt{2}}{3}$.