《2025年1课3练江苏人民出版社九年级数学下册北师大版》

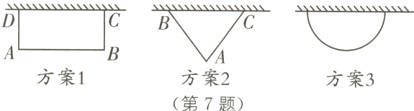
7. 九年级(2)班计划在劳动实践基地内种植蔬菜，班长买回来8米长的围栏，准备围成一边靠墙(墙足够长)的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案，最佳方案是（ ）.

A. 方案1
B. 方案2
C. 方案3
D. 方案1或方案2

答案： C [解析]方案1：设AD = x米，则AB = (8 - 2x)米，
菜园的面积为S = x(8 - 2x)=-2x^{2}+8x=-2(x - 2)^{2}+8，
∴当x = 2时，菜园的最大面积为8平方米；
方案2：当∠BAC = 90°时，菜园的最大面积为$\frac{1}{2}\times4\times4 = 8$（平方米）；
方案3：半圆的半径为$\frac{8}{\pi}$米，此时菜园面积为$\frac{\pi\times(\frac{8}{\pi})^{2}}{2}=\frac{32}{\pi}$（平方米）＞8平方米. 故选C.

8. (2023·天津中考)如图，要围一个矩形菜园ABCD，其中一边AD是墙，且AD的长不能超过26 m，其余的三边AB，BC，CD用篱笆，且这三边的和为40 m，有下列结论:①AB的长可以为6 m;②AB的长有两个不同的值满足菜园ABCD面积为192 m²;③菜园ABCD面积的最大值为200 m².其中，正确结论的个数是( ).

A. 0
B. 1
C. 2
D. 3

答案： C [解析]设AD边长为x m，则AB边长为$\frac{40 - x}{2}$m，
当AB = 6 m时，$\frac{40 - x}{2}=6$，解得x = 28.
∵AD的长不能超过26 m，
∴x≤26，故①不正确；
∵菜园ABCD的面积为192 m²，
∴$x\cdot\frac{40 - x}{2}=192$，整理，得$x^{2}-40x + 384 = 0$，
解得x = 24或x = 16，
∴AB的长有两个不同的值满足菜园ABCD的面积为192 m²，故②正确；
设矩形菜园的面积为y m²，
根据题意，得$y = x\cdot\frac{40 - x}{2}=-\frac{1}{2}(x^{2}-40x)=-\frac{1}{2}(x - 20)^{2}+200$.
∵$-\frac{1}{2}＜0$，20 ＜ 26，
∴当x = 20时，y有最大值，最大值为200. 故③正确.
∴正确的有2个. 故选C.
解后反思 本题主要考查了一元二次方程和二次函数的应用，读懂题意，找到等量关系准确地列出函数表达式和方程是解题的关键.

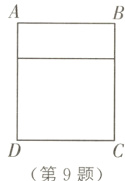
9. 如图，用一根60厘米的铁丝制作一个“日”字型框架ABCD，铁丝恰好全部用完.
(1)若所围成的矩形框架ABCD的面积为144平方厘米，则AB的长为多少厘米?
(2)矩形框架ABCD面积的最大值为________平方厘米.

答案：
(1)设框架的AB边长为x厘米，则AD边长为$\frac{60 - 3x}{2}$厘米，
∴$x\cdot\frac{60 - 3x}{2}=144$，解得x = 8或x = 12，均符合题意，
∴AB的长为8厘米或12厘米.
(2)150

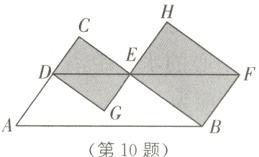
10. 中考新考法 动点问题 如图，在Rt△ABC中，∠C = 90°，BC = 4，BA = 5，点D为边AC上的一动点，过点D作DE//AB交边BC于点E，过点B作BF⊥BC交DE的延长线于点F，分别以DE，EF为对角线画矩形CDGE和矩形HEBF，则在D从A到C的运动过程中，当矩形CDGE和矩形HEBF的面积和最小时，EF的长度为________.

答案： $\frac{5}{2}$ [解析]在Rt△ABC中，∠C = 90°，BC = 4，BA = 5，
∴$AC=\sqrt{AB^{2}-BC^{2}} = 3$.
设DC = x，则AD = 3 - x.
∵DF//AB，
∴$\frac{DC}{AC}=\frac{CE}{BC}$，即$\frac{x}{3}=\frac{CE}{4}$，
∴$CE=\frac{4x}{3}$，
∴$BE = 4-\frac{4x}{3}$.
∵BF⊥BC，AC⊥BC，
∴AD//BF，
∴四边形ABFD是平行四边形，
∴BF = AD = 3 - x.
设S是矩形CDGE和矩形HEBF的面积和，
∴$S = S_{矩形CDGE}+S_{矩形HEBF}=DC\cdot CE+BF\cdot BE=x\cdot\frac{4x}{3}+(3 - x)(4-\frac{4x}{3})=\frac{8}{3}x^{2}-8x + 12$.
∵$\frac{8}{3}＞0$，
∴当$x = -\frac{-8}{2\times\frac{8}{3}}=\frac{3}{2}$时，S有最小值，
∴$BE = 4-\frac{4}{3}\times\frac{3}{2}=2$，$BF = 3-\frac{3}{2}=\frac{3}{2}$，
∴$EF=\sqrt{BE^{2}+BF^{2}}=\frac{5}{2}$.
故矩形CDGE和矩形HEBF的面积和最小时，EF的长度为$\frac{5}{2}$.