《2025年1课3练江苏人民出版社九年级数学下册北师大版》

7 (2024·北京西城区二模)下面问题中，y与x满足的函数关系是二次函数的是( ).
①面积为10 cm²的矩形中，矩形的长y(cm)与宽x(cm)的关系；
②在底面圆的半径为5 cm的圆柱中，侧面积y(cm²)与圆柱的高x(cm)的关系；
③某商品每件进价为80元，在某段时间内以每件x元出售，可卖出(100 - 2x)件。 利润y(元)与每件进价x(元)的关系。
A. ①
B. ②
C. ③
D. ①③

答案： C

8 (2024·广东中考)若点(0，y₁)，(1，y₂)，(2，y₃)都在二次函数y=x²的图象上，则( ).
A. y₃＞y₂＞y₁
B. y₂＞y₁＞y₃
C. y₁＞y₃＞y₂
D. y₃＞y₁＞y₂

答案： A

9 (2024·福建福州鼓楼区期末)函数y=ax - 2与y=ax²(a≠0)在同一平面直角坐标系中的图象可能是( ).

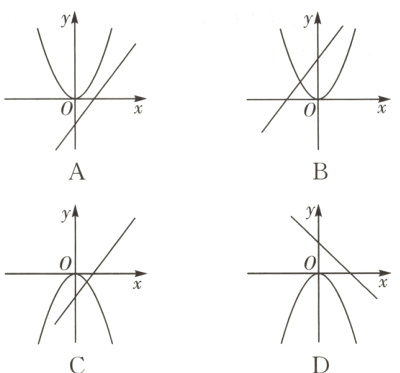
答案： A

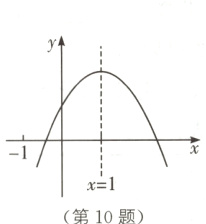
10 (2024·抚顺望花区模拟)已知二次函数y=ax²+bx+c的图象如图所示，有以下结论：
(1)直接写出a与b的关系：______.
(2)abc______0；9a+3b+c______0.（填“＞”“＜”或“=”）
(3)若点(-2，y₁)和(m，y₂)在该图象上，且y₁＞y₂，则m的取值范围是______.

答案：
(1)$2a + b = 0$
(2)$\lt$ $\lt$ [解析]由抛物线图象可知，$a\lt0$，$b\gt0$，$c\gt0$，$\therefore abc\lt0$。
　由图象的对称性可得$x = 3$和$x = - 1$时，$y$的取值相等，$\therefore$当$x = 3$时，$9a + 3b + c\lt0$。
(3)$m\lt-2$或$m\gt4$ [解析]当$x\lt1$时，$m\lt-2$；当$x\gt1$时，点$(-2,y_{1})$关于对称轴对称的点为$(4,y_{1})$，则$m\gt4$。

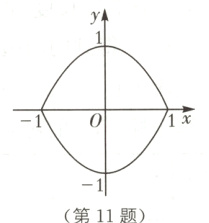
11 (2024·北京房山区模拟)平面直角坐标系xOy中，将抛物线y=x² - 1在x轴和x轴下方的部分记作G₁，将G₁沿x轴翻折记作G₂，G₁和G₂构成的图形记作G。 关于图形G，如图所示，以下三个结论中，正确的序号是______.
①图形G关于原点对称；
②图形G关于直线y=x对称；
③图形G的面积为S，满足2＜S＜π。

答案： ①③ [解析]由图形可知，图形$G$关于原点对称，不关于直线$y = x$对称，故①正确，②错误；
　如图，图形$G$的面积$S$大于$\triangle ABC$与$\triangle ABD$的面积之和，小于$\odot O$的面积。
　$\because S_{\triangle ABC}+S_{\triangle ABD}=\frac{1}{2}\times2\times1+\frac{1}{2}\times2\times1 = 2$，$S_{\odot O}=\pi\times1^{2}=\pi$，$\therefore$图形$G$的面积满足$2\lt S\lt\pi$，故③正确。

12 (2024·北京三帆中学模拟)在平面直角坐标系xOy中，点M(1，m)，N($\frac{t}{2}$，n)是抛物线y=a(x - t)²(a＞0)上的两点(M，N不重合)。
(1)若m=n，求t的值；
(2)若点P(x₀，p)在抛物线上，且对于t + 1＜x₀＜t + 2都有n＜p＜m，求t的取值范围。

答案：
(1)$\because m = n$，且抛物线过点$M(1,m)$，$N(\frac{t}{2},n)$，
　$\therefore$对称轴是直线$x = t=\frac{1+\frac{t}{2}}{2}$，$\therefore t=\frac{2}{3}$。
(2)$\because$抛物线$y = a(x - t)^{2}(a\gt0)$，
　$\therefore$抛物线开口向上，对称轴为直线$x = t$。
　$\because$点$P(x_{0},p)$在抛物线上，且$t + 1\lt x_{0}\lt t + 2$，
　$\therefore$点$P(x_{0},p)$在对称轴的右侧，
　$\therefore$点$P(x_{0},p)$关于对称轴的对称点为$(2t - x_{0},p)$。
　①当$t\leqslant0$时，$\because n\lt p\lt m$，
　$\therefore\begin{cases}t + 2\leqslant1\\t + 1\geqslant\frac{t}{2}\end{cases}$，$\therefore-2\leqslant t\leqslant-1$；
　②当$t\gt0$时，存在当$0\lt t\leqslant1$时，$t + 1\gt1$，则$p\gt m$与已知矛盾，故不符合题意。
　综上所述，$t$的取值范围是$-2\leqslant t\leqslant-1$。