《2025年1课3练江苏人民出版社九年级数学下册北师大版》

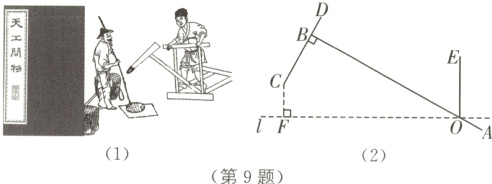
9 传统文化 《天工开物》(2024·湖南中考)如图，图(1)为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图，图(2)为其平面示意图. 已知AB⊥CD于点B，AB与水平线l相交于点O，OE⊥l. 若BC = 4分米，OB = 12分米，∠BOE = 60°，则点C到水平线l的距离CF为______分米(结果用含根号的式子表示).

答案：
(6 - 2√3) [解析]如图，延长DC交l于点M，连接OC.

在Rt△OBM中，∠BOM = 90° - 60° = 30°，OB = 12分米，
∴BM = 12×tan 30° = 4√3（分米），OM = 12/cos 30° = 12/(√3/2) = 8√3（分米）.
∵S△OBM = S△OCM + S△OBC，
∴1/2OB·BM = 1/2OM·CF + 1/2OB·BC，
∴1/2×12×4√3 = 1/2×8√3×CF + 1/2×12×4，
∴CF = (24√3 - 24)/(4√3) = (6 - 2√3)分米.
一题多解：过点B作BG⊥l于点G，过点C作CH⊥BG于点H.
∵AB⊥CD，OE⊥l，BG⊥l，∠BOE = 60°，
∴BG//OE，
∴∠OBG = ∠BOE = 60°.
在Rt△OBG中，∠BOG = 90° - 60° = 30°，OB = 12分米，
∴BG = 12×sin 30° = 6（分米）.
在Rt△BCH中，∠CBG = 90° - 60° = 30°，BC = 4分米，
∴BH = 4×cos 30° = 2√3（分米），
∴HG = BG - BH = (6 - 2√3)分米.
在矩形CFGH中，CF = HG = (6 - 2√3)分米.

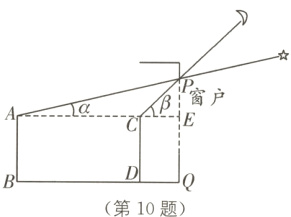
10 (2024·河北中考)中国的探月工程激发了同学们对太空的兴趣. 某晚，淇淇在家透过窗户的最高点P恰好看到一颗星星，此时淇淇距窗户的水平距离BQ = 4 m，仰角为α；淇淇向前走了3 m后到达点D，透过点P恰好看到月亮，仰角为β，如图是示意图. 已知，淇淇的眼睛与水平地面BQ的距离AB = CD = 1.6 m，点P到BQ的距离PQ = 2.6 m，AC的延长线交PQ于点E. (注：图中所有点均在同一平面)
(1)求β的大小及tanα的值；
(2)求CP的长及sin∠APC的值.
　　　　　　　　

答案：

(1)由题意，得PQ⊥AE，PQ = 2.6 m，AB = CD = EQ = 1.6 m，AE = BQ = 4 m，AC = BD = 3 m，
∴CE = 4 - 3 = 1(m)，PE = 2.6 - 1.6 = 1(m)，∠CEP = 90°，
∴CE = PE，
∴β = ∠PCE = 45°，tan α = tan∠PAE = PE/AE = 1/4.
(2)
∵CE = PE = 1 m，∠CEP = 90°，
∴CP = √(1² + 1²) = √2(m).
如图，过点C作CH⊥AP于点H.
∵tan α = tan∠PAE = CH/AH = 1/4，
∴设CH = x m，则AH = 4x m.
∴x² + (4x)² = AC² = 9.
∴x = 3√17/17.
∴CH = 3√17/17.
∴sin∠APC = CH/CP = (3√17/17)/√2 = 3√34/34.

方法诠释：本题考查了解直角三角形.在生活情境中抽象出几何图形，添加辅助线，构造直角三角形，再利用三角函数和勾股定理计算求解.

11 新情境 数学与生活融合 (2023·嘉兴中考)图(1)是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别)，其示意图如图(2)，摄像头A的仰角、俯角均为15°，摄像头高度OA = 160 cm，识别的最远水平距离OB = 150 cm.
　　
(1)身高208 cm的小杜，头部高度为26 cm，他站在离摄像头水平距离130 cm的点C处，请问小杜最少需要下蹲多少厘米才能被识别?
(2)身高120 cm的小若，头部高度为15 cm，踮起脚尖可以增高3 cm，但仍无法被识别，社区及时将摄像头的仰角、俯角都调整为20°(如图(3))，此时小若能被识别吗? 请计算说明. (精确到0.1 cm，参考数据：sin 15°≈0.26，cos 15°≈0.97，tan 15°≈0.27，sin 20°≈0.34，cos 20°≈0.94，tan 20°≈0.36)

答案：

(1)如图
(1)，过点C作OB的垂线分别交仰角、俯角线于点E，D，交水平线于点F.
在Rt△AEF中，tan∠EAF = EF/AF，
∴EF = AF·tan 15°≈130×0.27 = 35.1(cm).
∵∠EAF = ∠DAF，AF = AF，∠AFE = ∠AFD = 90°，
∴△ADF≌△AEF(ASA)，
∴EF = DF = 35.1 cm，
∴CE = 160 + 35.1 = 195.1(cm)，
208 - 195.1 = 12.9(cm).
故小杜最少需要下蹲12.9 cm才能被识别.

(2)如图
(2)，过B作OB的垂线分别交仰角、俯角线于点M，N，交水平线于点P.
在Rt△APM中，tan∠MAP = MP/AP，
∴MP = AP·tan 20°≈150×0.36 = 54.0(cm).
∵∠MAP = ∠NAP，AP = AP，∠APM = ∠APN = 90°，
∴△AMP≌△ANP(ASA)，
∴PN = MP = 54.0 cm，
∴BN = 160 - 54.0 = 106.0(cm).
∵小若踮起脚尖后头顶的高度为120 + 3 = 123(cm)，
∴小若头顶超出点N的高度为123 - 106.0 = 17.0(cm)＞15 cm，
∴踮起脚尖小若能被识别.