《2025年1课3练江苏人民出版社九年级数学下册北师大版》

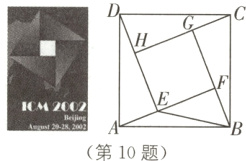
10. 传统文化 赵爽弦图 (2023·杭州中考)第二十四届国际数学家大会会徽的设计基础是1 700多年前中国古代数学家赵爽的“弦图”. 如图，在由四个全等的直角三角形(△DAE，△ABF，△BCG，△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD中，∠ABF＞∠BAF，连接BE. 设∠BAF = α，∠BEF = β，若正方形EF - GH与正方形ABCD的面积之比为1∶n，tanα = tan²β，则n等于( )．


A. 5
B. 4
C. 3
D. 2

答案： C　[解析]设$AE = a$，$DE = b$，则$BF = a$，$AF = b$．
∵$\tan\alpha=\frac{a}{b}$，$\tan\beta=\frac{a}{b - a}$，$\tan\alpha=\tan^{2}\beta$，
∴$\frac{a}{b}=(\frac{a}{b - a})^{2}$，
∴$(b - a)^{2}=ab$，
∴$a^{2}+b^{2}=3ab$．
∵$a^{2}+b^{2}=AD^{2}=S_{正方形ABCD}$，$(b - a)^{2}=S_{正方形EFGH}$，
∴$S_{正方形EFGH}:S_{正方形ABCD}=ab:3ab = 1:3$．
∵$S_{正方形EFGH}:S_{正方形ABCD}=1:n$，
∴$n = 3$．故选C.

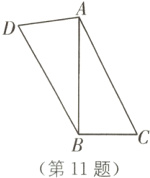
11. (2024·南京鼓楼区三模)如图，在△ABC中，∠ABC = 90°，tan∠BAC = $\frac{1}{2}$，AD = 2，BD = 4，连接CD，则CD长的最大值为________．
　　　　　　　　　　　　　

答案：
$1 + 2\sqrt{5}$　[解析]如图，在$AD$的下方作$Rt\triangle ADT$，使得$\angle ADT = 90^{\circ}$，$DT = 1$，连接$CT$，$AT$，则$AT=\sqrt{5}$．　　　　　　　　　　　　　　
∵$\frac{AD}{DT}=\frac{2}{1}=2$，$\tan\angle BAC=\frac{BC}{AB}=\frac{1}{2}$，
∴$\frac{AD}{DT}=\frac{AB}{BC}$，即$\frac{AD}{AB}=\frac{DT}{BC}$．
∵$\angle ADT=\angle ABC = 90^{\circ}$，
∴$\triangle ADT\sim\triangle ABC$，
∴$\angle DAT=\angle BAC$，$\frac{AD}{AB}=\frac{AT}{AC}$，
∴$\angle DAB=\angle TAC$，$\frac{AD}{AT}=\frac{AB}{AC}$，
∴$\triangle DAB\sim\triangle TAC$，
∴$\frac{DB}{TC}=\frac{AD}{AT}=\frac{2}{\sqrt{5}}$．
∵$BD = 4$，
∴$TC = 2\sqrt{5}$．
∵$CD\leqslant DT + CT$，
∴$CD\leqslant1 + 2\sqrt{5}$，
∴$CD$长的最大值为$1 + 2\sqrt{5}$．归纳总结 本题考查了解直角三角形和相似三角形的综合应用，解题的关键是添加辅助线，构造相似三角形解决问题.

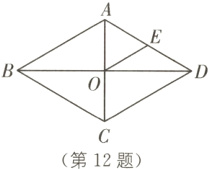
12. (2023·连云港中考)如图，菱形ABCD的对角线AC，BD相交于点O，E为AD的中点，AC = 4，OE = 2. 求OD的长及tan∠EDO的值.
　　　　　　　　　　　

答案：
∵四边形$ABCD$是菱形，
∴$AC\perp BD$，$OA=\frac{1}{2}AC$．
∵$AC = 4$，
∴$OA = 2$．
∵$E$为$AD$的中点，
∴$OE=\frac{1}{2}AD$．
∵$OE = 2$，
∴$AD = 4$，
∴$OD=\sqrt{AD^{2}-OA^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$，
∴$\tan\angle EDO=\frac{AO}{OD}=\frac{2}{2\sqrt{3}}=\frac{\sqrt{3}}{3}$．

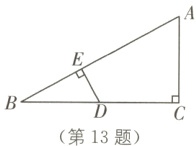
13. 原创素养题 运算能力 如图，在Rt△ABC中，∠C = 90°，点D是BC的中点，DE⊥AB，垂足为E，且tan B = $\frac{1}{2}$，AC = 1，求AE的长.
　

答案： 在$Rt\triangle ABC$中，
∵$AC = 1$，$\tan B=\frac{1}{2}$，
∴$\frac{AC}{BC}=\frac{1}{BC}=\frac{1}{2}$，
∴$BC = 2$，
∴$AB=\sqrt{5}$．
∵$D$为$BC$的中点，
∴$BD = 1$．在$Rt\triangle BED$中，$\tan B=\frac{DE}{BE}=\frac{1}{2}$，
∴设$DE = x$，则$BE = 2x$，由勾股定理，得$x^{2}+(2x)^{2}=1$，解得$x=\frac{\sqrt{5}}{5}$(负值舍去)，则$BE=\frac{2\sqrt{5}}{5}$，
∴$AE = AB - BE=\frac{3\sqrt{5}}{5}$．

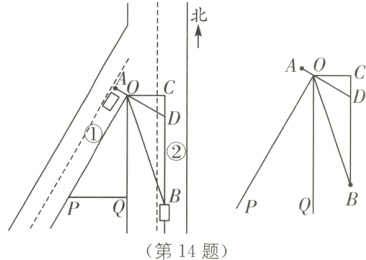
14. 新情境 测算交叉路口 (2023·株洲中考)如图所示，在某交叉路口，一货车在道路①上点A处等候“绿灯”，一辆轿车从被山峰POQ遮挡的道路②的点B处由南向北行驶. 已知∠POQ = 30°，BC//OQ，OC⊥OQ，AO⊥OP，线段AO的延长线交直线BC于点D.
(1)求∠COD的大小；
(2)若在点B处测得点O在北偏西α方向上，其中tanα = $\frac{\sqrt{3}}{5}$，OD = 12米. 问：该轿车至少行驶多少米才能发现点A处的货车? (当该轿车行驶至点D处时，正好发现点A处的货车)
　　　　　

答案：
(1)
∵$AO\perp OP$，
∴$\angle POD = 90^{\circ}$．
∵$\angle POQ = 30^{\circ}$，
∴$\angle DOQ=\angle POD-\angle POQ = 90^{\circ}-30^{\circ}=60^{\circ}$．
∵$OC\perp OQ$，
∴$\angle COQ = 90^{\circ}$，
∴$\angle COD=\angle COQ-\angle DOQ = 90^{\circ}-60^{\circ}=30^{\circ}$．
(2)
∵$BC// OQ$，$\angle COQ = 90^{\circ}$，
∴$\angle BCO = 180^{\circ}-\angle COQ = 90^{\circ}$．在$Rt\triangle COD$中，$\angle COD = 30^{\circ}$，$OD = 12$米，
∴$CD=\frac{1}{2}OD = 6$米，
∴$OC=\sqrt{OD^{2}-CD^{2}}=\sqrt{12^{2}-6^{2}} = 6\sqrt{3}$(米)．
∵$\tan\alpha=\tan\angle OBC=\frac{\sqrt{3}}{5}=\frac{OC}{BC}$，
∴$BC=\frac{OC}{\tan\alpha}=6\sqrt{3}\div\frac{\sqrt{3}}{5}=30$(米)，
∴$BD = BC - CD = 30 - 6 = 24$(米)．故该轿车至少行驶24米才能发现点$A$处的货车.