《2025年1课3练江苏人民出版社九年级数学下册北师大版》

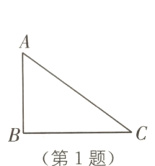
1. 教材P4随堂练习T1·改编 (2024·云南中考)如图，在△ABC中，若∠B = 90°，AB = 3，BC = 4，则tan A的值为( )．
A. $\frac{4}{5}$ B. $\frac{3}{5}$ C. $\frac{4}{3}$ D. $\frac{3}{4}$
　　

答案： C

2. (2024·江苏扬州江都区期末)在Rt△ABC中，∠C = 90°，若各边都扩大3倍，则tan A的值( )．
A. 缩小$\frac{1}{3}$
B. 扩大3倍
C. 不变
D. 不能确定

答案： C

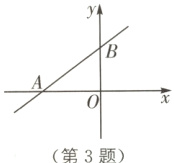
3. 如图，直线$y=\frac{3}{4}x + 3$与x轴、y轴分别交于A，B两点，则tan∠BAO的值是________．
　　

答案： $\frac{3}{4}$　[解析]令$x = 0$，则$y = 3$；令$y = 0$，则$x = - 4$，
∴直线$y=\frac{3}{4}x + 3$与$x$轴、$y$轴的交点坐标分别为$A(-4,0)$，$B(0,3)$，
∴$OA = 4$，$OB = 3$，
∴$\tan\angle BAO=\frac{BO}{AO}=\frac{3}{4}$．

4. 教材P2想一想·拓展 如图，下面四个梯子最陡的是( )．
　　
　　　　

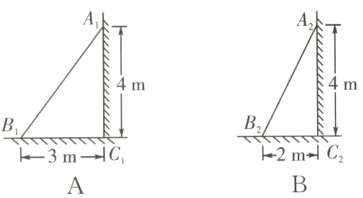
答案： B

5. 教材P3例1·改编 如图，A，B两个梯子相比，梯子________更陡.
　　　　　　　　　　　　　　　　　

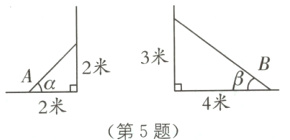
答案： A

6. 教材P4习题T1·变式 如图，A，B，C三点在正方形网格线的交点处，若将△ACB绕着点A逆时针旋转得到△AC'B'，则tan B'的值为( )．
A. $\frac{1}{2}$ B. $\frac{1}{3}$ C. $\frac{1}{4}$ D. $\frac{\sqrt{2}}{4}$
　　　　　　　　　　　　　 　　　

答案： B

7. (2024·山东济南历城区期末)有6个大小相同的小正方形，恰好如图所示放置在△ABC中，则tan B的值等于________．

答案：
$\frac{1}{2}$　[解析]如图.　　　　　 依题意，得$FH// BC$，$EH = 1$，$FH = 2$，$\angle EHF = 90^{\circ}$，
∴$\angle B=\angle EFH$，
∴$\tan B=\tan\angle EFH=\frac{EH}{FH}=\frac{1}{2}$．归纳总结 本题考查了平行线的性质与正切，解题的关键是利用平行线和垂直，构造直角三角形，求正切值.

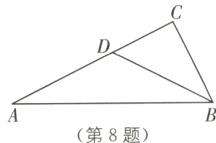
8. 教材P4随堂练习T1·变式 如图，在Rt△ABC中，∠C = 90°，D为AC上的一点，CD = 3，AD = BD = 5.求tan A的值.
　　　　　　　　　　　　　　　　　　　　　　　

答案： 在$Rt\triangle BCD$中，
∵$CD = 3$，$AD = BD = 5$，
∴$BC=\sqrt{BD^{2}-CD^{2}}=\sqrt{5^{2}-3^{2}} = 4$，$AC = 5 + 3 = 8$，
∴$\tan A=\frac{BC}{AC}=\frac{4}{8}=\frac{1}{2}$．

9. 新情境 参加冬奥雪上项目 (2024·德州模拟)雪上项目占据了2022年北京冬奥会的大部分比赛项目，有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等. 如图，某滑雪运动员在坡度为5∶12的雪道上下滑65 m，则该滑雪运动员沿竖直方向下降的高度为( )．
A. 13 m B. 25 m C. $\frac{325}{12}$ m D. 156 m
　　 　

答案：
B　[解析]如图，　　　　　　　 由题意，得$AB = 65m$，$BC\perp AC$于点$C$．
∵斜坡$AB$的坡度是$5:12$，
∴设$BC = 5a m$，则$AC = 12a m$，由勾股定理，得$AB=\sqrt{(5a)^{2}+(12a)^{2}} = 13a(m)$，
∴$13a = 65$，解得$a = 5$，
∴$BC = 5a = 25m$．故选B.