《2025年1课3练江苏人民出版社九年级数学下册北师大版》

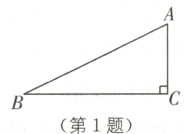
1 教材P13想一想·拓展（2024·淄博高青二模）如图，在△ABC中，∠ACB = 90°，∠ABC = 26°，BC = 6.若用科学计算器求边AC的长，则下列按键顺序正确的是（ ）.
　　　　　　

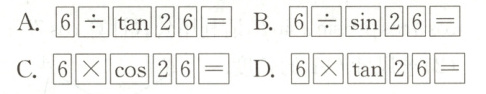
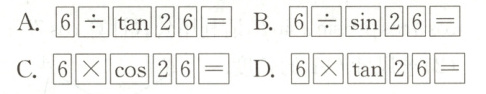
答案： D[解析]在Rt△ABC中，
∵tan∠ABC = $\frac{AC}{BC}$，
∴AC = BC·tan∠ABC = 6×tan 26°。故选D。
思路引导 本题考查了用科学计算器计算三角函数值。利用直角三角形的边和角之间的关系用BC和tan∠ABC表示出AC，熟练掌握计算器面板符号的含义及计算器的使用方法从而求AC的长。

2 教材P14随堂练习T1·改编 用计算器求下列三角函数值.（精确到0.0001）
（1）sin 38°19′≈________，sin 63°24′9″≈________；
（2）cos 78°36′16″≈________，cos 12°29′≈________；
（3）tan 43°9′15″≈________，tan 40°10′≈________.

答案：
(1)0.6200　0.8942
(2)0.1976　0.9764
(3)0.9376　0.8441

3 已知sin α = 0.3，cos β = 0.6，则α + β =________（精确到1′）.

答案： 70°35'

4 教材P14随堂练习T2·改编 用计算器求锐角α的值.
（1）已知sin α = 0.8310，则锐角α≈________°________′________″；
（2）已知cos α = 0.9511，则锐角α≈________°________′________″；
（3）已知tan α = 3.8726，则锐角α≈________°________′________″.

答案：
(1)56　12　6　
(2)17　59　31　
(3)75　31　16

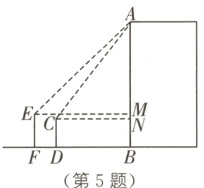
5 新情境 测量电子厂高度（2024·深圳中考）如图，为了测量某电子厂的高度，小明用高1.8 m的测量仪EF测得顶端A的仰角为45°，小军在小明的前面5 m处用高1.5 m的测量仪CD测得顶端A的仰角为53°，则电子厂AB的高度为（ ）.（参考数据：sin 53°≈$\frac{4}{5}$，cos 53°≈$\frac{3}{5}$，tan 53°≈$\frac{4}{3}$）
　　　　　　
A. 22.7 m
B. 22.4 m
C. 21.2 m
D. 23.0 m

答案： A[解析]由题意,得EF = BM = 1.8m,CD = BN = 1.5m,DF = 5m,EM = BF,BD = CN,EM⊥AB,CN ⊥AB.
设BD = CN = xm,
则EM = BF = DF + BD = (x + 5)m.
在Rt△AEM中,∠AEM = 45°,
∴AM = EM·tan45° = (x + 5)m.
在Rt△ACN中,∠ACN = 53°,
∴AN = CN·tan53°≈$\frac{4}{3}x$m.
∵AM + BM = AN + BN = AB,
∴x + 5 + 1.8 = $\frac{4}{3}x$ + 1.5,解得x = 15.9,
∴AN = $\frac{4}{3}$×15.9 = 21.2(m),
∴AB = AN + BN = 21.2 + 1.5 = 22.7(m).
故电子厂AB的高度为22.7m.故选A.

6 如图是自动卸货汽车卸货时的示意图.汽车的车厢采用液压机构、车厢的支撑顶杆BC的底部支撑点B在水平线AD的下方，AB与水平线AD之间的夹角是5°，卸货时，车厢AC与水平线AD成60°，此时AB与支撑顶杆BC的夹角为45°，若AC = 2米，则BC的长度为________米.（结果保留一位小数，参考数据：sin 65°≈0.91，cos 65°≈0.42，tan 65°≈2.14，sin 70°≈0.94，cos 70°≈0.34，tan 70°≈2.75，$\sqrt{2}$≈1.41）
　　　　　　

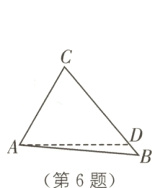
答案：
2.6　[解析]如图,过点C作CF⊥AB于点F.
在Rt△ACF中,sin∠CAF = $\frac{CF}{AC}$,
∴CF = AC·sin65°≈2×0.91 = 1.82(米).
在Rt△BCF中,∠ABC = 45°,
∴BC = $\sqrt{2}$CF≈1.41×1.82≈2.6(米).

7 教材P15习题T4·变式（2024·甘孜州中考）如图，一艘海轮位于灯塔P的北偏东37°方向，距离灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处.这时，B处距离A处有多远?（参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）
　　　　　　　　　　　　　　　　

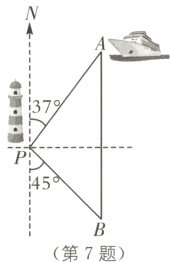
答案： 过点P作PC⊥AB于点C.
在Rt△APC中,
∵∠A = 37°,AP = 100海里，
∴PC = AP·sinA = 100×sin37°≈100×0.60 = 60(海里),AC = AP·cos37°≈100×0.80 = 80(海里).
在Rt△PBC中，
∵∠B = 45°,
∴BC = PC = 60海里，
∴AB = AC + BC = 80 + 60 = 140(海里).
故B处距离A处有140海里.