《2025年1课3练江苏人民出版社九年级数学下册北师大版》

8 (江苏南京外国语学校特长生)如图，在Rt△ABC中，AC = 15，BC = 20，AM = 2CM，CD⊥AB，I为△BCD的内心，则IM = ________.

答案：
$\sqrt{65}$　　[解析]如图,过点I作IE⊥BC于点E,IF⊥CD于点F,IG⊥AB于点G,IH⊥AC于点H,连接BI.
　　　　　　　
∵I为△BCD的内心，
∴IE=IF=IG.
∵BI=BI,IG=IE,
∴Rt△BIG≌Rt△BIE(HL),
∴BE=BG.
　同理可得DG=DF,CF=CE.
∵CD⊥AB,
∴四边形DGIF是正方形，
∴DG=DF=IG.
∵AC⊥BC,
∴四边形IECH是矩形，
∴CH=IE,IH=EC.
　在Rt△ABC中,AC=15,BC=20,
∴AB=$\sqrt{AC^{2}+BC^{2}}$=$\sqrt{15^{2}+20^{2}}$=25.
∵AB·CD=AC·BC,
∴25CD=15×20,
∴CD=12,
∴BD=$\sqrt{BC^{2}-CD^{2}}$=$\sqrt{20^{2}-12^{2}}$=16.
∵DB+DC−BC=DG+BG+DF+FC−(BE+CE)=16+12−20=8,
∴2DG=8,
∴DG=4.
　同理可得2CE=BC+CD−BD=20+12−16=16,
∴CE=8,
∴IE=DG=4,IH=CE=8,
∴CH=IE=4.
∵AM=2CM,
∴CM=$\frac{1}{3}$AC=$\frac{1}{3}$×15=5,
∴MH=CM−CH=5−4=1,
∴IM=$\sqrt{MH^{2}+HI^{2}}$=$\sqrt{1^{2}+8^{2}}$=$\sqrt{65}$.

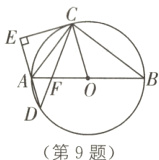
9 (2023·武威中考)如图，△ABC内接于⊙O，AB是⊙O的直径，D是⊙O上的一点，CO平分∠BCD，CE⊥AD，垂足为E，AB与CD相交于点F.
（1）求证：CE是⊙O的切线；
（2）当⊙O的半径为5，sin B = $\frac{3}{5}$时，求CE的长.

答案：
(1)
∵CE⊥AD,
∴∠E=90°.
∵CO平分∠BCD,
∴∠OCB=∠OCD.
∵OB=OC,
∴∠B=∠BCO=∠D,
∴∠D=∠OCD,
∴OC//DE,
∴∠OCE=180°−∠E=90°,
　又OC是⊙O的半径，
∴CE是⊙O的切线.
(2)
∵AB是⊙O的直径，
∴AB=10,∠ACB=90°.
在Rt△ABC中,sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴AC=$\frac{3}{5}$AB=6.
∵∠ACO+∠OCB=∠ACO+∠ACE=90°,
∴∠ACE=∠OCB=∠B,
∴sin∠ACE=sinB=$\frac{AE}{AC}$=$\frac{3}{5}$,
∴AE=$\frac{3}{5}$AC=$\frac{18}{5}$,
∴CE=$\sqrt{AC^{2}-AE^{2}}$=$\frac{24}{5}$.

10 (2023·福建中考)如图，已知△ABC内接于⊙O，CO的延长线交AB于点D，交⊙O于点E，交⊙O的切线AF于点F，且AF//BC.
（1）求证：AO//BE；
（2）求证：AO平分∠BAC.

答案：
(1)
∵AF是⊙O的切线，
　
∴AF⊥OA,即∠OAF=90°.
　
∵CE是⊙O的直径，
∴∠CBE=90°,
　
∴∠OAF=∠CBE.
　
∵AF//BC,
∴∠BAF=∠ABC,
　
∴∠OAF−∠BAF=∠CBE−∠ABC,
　　即∠OAB=∠ABE,
∴AO//BE.
(2)
∵∠ABE与∠ACE都是$\overset{\frown}{EA}$所对的圆周角，
　
∴∠ABE=∠ACE.
　
∵OA=OC,
　
∴∠ACE=∠OAC,
∴∠ABE=∠OAC.
　　由
(1)知,∠OAB=∠ABE,
∴∠OAB=∠OAC,
　
∴AO平分∠BAC.
　解后反思　　本题考查了切线的性质、角平分线的定义、平行线的判定与性质、等腰三角形的性质，熟练掌握切线的性质是解题的关键.

11 中考新考法 解题方法型阅读理解题 阅读材料：如图（1），△ABC的周长为l，内切圆O的半径为r，连接OA，OB，OC，△ABC被划分为三个小三角形，用S△ABC表示△ABC的面积.
∵S△ABC = S△OAB + S△OBC + S△OCA，
又S△OAB = $\frac{1}{2}$AB·r，S△OBC = $\frac{1}{2}$BC·r，S△OCA = $\frac{1}{2}$CA·r，
∴S△ABC = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$CA·r = $\frac{1}{2}$l·r.（可作为三角形内切圆的半径公式）
（1）理解与应用：利用公式计算边长分别为5，12，13的三角形内切圆半径；
（2）类比与推理：若四边形ABCD存在内切圆（与各边都相切的圆，如图（2））且面积为S，各边长分别为a，b，c，d，试推导四边形内切圆的半径公式；
（3）拓展与延伸：若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a1，a2，a3，…，an，合理猜想其内切圆的半径公式(不需要说明理由).

答案：
(1)
∵三角形三边长为5,12,13,5²+12²=13²,
∴这个三角形为直角三角形，
∴S_{△ABC}=$\frac{1}{2}$×5×12=30,l=5+12+13=30.
　　由S_{△ABC}=$\frac{1}{2}$lr,得r=$\frac{2S_{△ABC}}{l}$=2.
(2)连接OA,OB,OC,OD.
∵S_{四边形ABCD}=S_{△OAB}+S_{△OBC}+S_{△OCD}+S_{△OAD},S_{△OAB}=$\frac{1}{2}$AB·r,S_{△OBC}=$\frac{1}{2}$BC·r,S_{△OCD}=$\frac{1}{2}$CD·r,S_{△OAD}=$\frac{1}{2}$AD·r,
∴S=$\frac{1}{2}$AB·r+$\frac{1}{2}$BC·r+$\frac{1}{2}$CD·r+$\frac{1}{2}$AD·r=$\frac{1}{2}$r·(AB+BC+CD+AD).
　　即r=$\frac{2S}{AB+BC+CD+AD}$=$\frac{2S}{a + b + c + d}$.
(3)r=$\frac{2S}{a_{1}+a_{2}+\cdots+a_{n}}$.