《2025年1课3练江苏人民出版社九年级数学下册北师大版》

1 如图，△ABC的内切圆与三边分别相切于点D，E，F，若∠B = 50°，则∠EDF = ________度.

答案：
65　　[解析]如图，设△ABC的内切圆圆心为O,连接OE,OF.
　　　　　　　　
∵△ABC的内切圆与三边分别相切于点D,E,F，
∴OE⊥AB,OF⊥BC,
∴∠OEB=∠OFB=90°.
∵∠B=50°,
∴∠EOF=360°−90°−90°−50°=130°,
∴∠EDF=$\frac{1}{2}$∠EOF=65°.

2 教材P92例2·改编 尺规作图.（要求：用尺规作图，保留作图痕迹，不写作法，不要求证明）
（1）如图（1），已知△ABC. 求作：△ABC的内切圆⊙I；
（2）如图（2），点C，D分别在∠AOB的两边上，用直尺和圆规作一个圆，和OA，OB，CD都相切.

答案：

(1)作△ABC两个角的平分线交于点I,作IE⊥BC 于点E,以点I为圆心,IE为半径作⊙I.
　　　　　　　
(2)有两种情况:①作∠ACD,∠BDC,∠AOB三个角中任意两个角的平分线交于点I,作IE⊥CD于点E，以点I为圆心，IE为半径作⊙I.②作∠OCD，∠CDO,∠AOB三个角中任意两个角的平分线交于点I',作I'E'⊥CD于点E',以点I'为圆心,I'E'为半径作⊙I'.图略.

3 以下说法正确的是( ).
①锐角三角形的内心在三角形内部；
②直角三角形的内心是斜边的中点；
③钝角三角形的外心在三角形外，靠近最长边；
④三角形的内心是到三个顶点距离相等的点.
A. ①③
B. ③④
C. ①②③
D. ②③④

答案： A

4 (2023·广州中考)如图，△ABC的内切圆⊙I与BC，CA，AB分别相切于点D，E，F，若⊙I的半径为r，∠A = α，则(BF + CE - BC)的值和∠FDE的大小分别为( ).

A. 2r，90° - α
B. 0，90° - α
C. 2r，90° - $\frac{\alpha}{2}$
D. 0，90° - $\frac{\alpha}{2}$

答案： D

5 教材P93习题T2·改编 (2024·南充一模)如图，点O是△ABC外接圆的圆心，点I是△ABC的内心，连接OB，IA. 若∠CAI = 37°，则∠OBC的度数为( ).

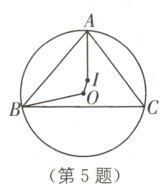
A. 37°
B. 20°
C. 16°
D. 14°

答案： C

6 教材P107复习题T22·变式 (2023·威海中考)在△ABC中，BC = 3，AC = 4，下列说法错误的是( ).
A. 1＜AB＜7
B. S△ABC≤6
C. △ABC内切圆的半径r＜1
D. 当AB = $\sqrt{7}$时，△ABC是直角三角形

答案： C

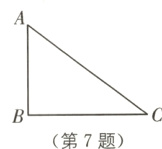
7 教材P105复习题T10·变式 如图，王奶奶有一块三角形的布料，∠ABC = 90°，她要裁一个圆片，已知AB = 60 cm，BC = 80 cm，为了充分地利用这块布料，使剪下来的圆片的直径尽量大些，她应该怎样裁剪？这个圆的直径是多少?

答案：
∵AB=60cm,BC=80cm,
∴AC=100cm,
∴面积S=$\frac{1}{2}$×60×80=2400(cm²),周长C=60+80+100=240(cm).
　由r=$\frac{2S}{C}$,得r=$\frac{4800}{240}$=20(cm).
　王奶奶的做法是:在BC上取点D,使BD=20cm,以BD为边在△ABC内作正方形BDOE,以O为圆心20cm长为半径作圆，则剪下来的圆片的直径最大，此时圆的直径为40cm.